Next: Miscellaneous Exercises Up: Some More Special Matrices Previous: Submatrix of a Matrix Contents
Let ![]() be an
be an
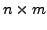 matrix and
matrix and ![]() be an
be an
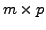 matrix.
Suppose
matrix.
Suppose ![]() Then, we can decompose the matrices
Then, we can decompose the matrices ![]() and
and ![]() as
as
![]() and
and
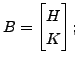 where
where ![]() has order
has order
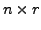 and
and ![]() has order
has order
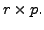 That is, the matrices
That is, the matrices ![]() and
and ![]() are submatrices of
are submatrices of ![]() and
and ![]() consists of the first
consists of the first ![]() columns of
columns of ![]() and
and ![]() consists of the last
consists of the last 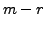 columns of
columns of ![]() .
Similarly,
.
Similarly, ![]() and
and ![]() are submatrices of
are submatrices of ![]() and
and ![]() consists of the first
consists of the first ![]() rows of
rows of ![]() and
and ![]() consists of the last
consists of the last ![]() rows of
rows of ![]() . We now prove the following
important theorem.
. We now prove the following
important theorem.
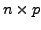 . The
matrix products
. The
matrix products 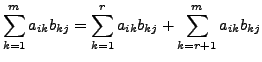 |
|||
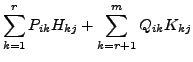 |
|||
Theorem 1.3.5 is very useful due to the following reasons:
For example, if
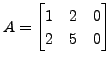 and
and
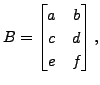 Then
Then
![$\displaystyle A B = \begin{bmatrix}1& 2 \\ 2& 5
\end{bmatrix} \begin{bmatrix}a&...
...ght] =
\begin{bmatrix}a + 2 c & b + 2 d \\ 2 a + 5 c & 2 b + 5 d \end{bmatrix}.$](img230.png)
If
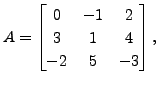 then
then ![]() can be decomposed as
follows:
can be decomposed as
follows:
![$ A = \left[\begin{array}{c\vert cc} 0 & -1 & 2 \\ 3 & 1 & 4 \\ \hline -2 & 5
& -3 \end{array}\right],$](img232.png) or
or
![$ \;\;\; A= \left[\begin{array}{cc\vert c} 0 & -1 & 2 \\ 3 & 1 & 4 \\ \hline -2 & 5 &
-3 \end{array}\right],$](img233.png) or
or
![$ A=\left[\begin{array}{cc\vert c} 0 & -1 & 2 \\
\hline 3 & 1 & 4 \\ -2 & 5 &
-3 \end{array}\right]$](img234.png) and so on.
and so on.
Suppose
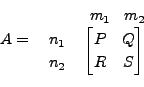 and
and
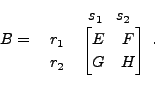 Then the matrices
Then the matrices
![]() and
and
![]() are
called the blocks of the matrices
are
called the blocks of the matrices
![]() and
and ![]() respectively.
respectively.
Even if ![]() is defined, the orders of
is defined, the orders of ![]() and
and ![]() may not be same and hence, we may not be able to add
may not be same and hence, we may not be able to add ![]() and
and ![]() in
the block form. But, if
in
the block form. But, if ![]() and
and ![]() is defined then
is defined then
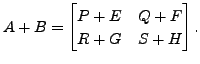
Similarly, if the product ![]() is defined, the product
is defined, the product ![]() need not be
defined. Therefore, we can talk of matrix product
need not be
defined. Therefore, we can talk of matrix product ![]() as block product of
matrices, if both the products
as block product of
matrices, if both the products ![]() and
and ![]() are defined. And in this case, we have
are defined. And in this case, we have
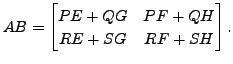
That is, once a partition of ![]() is fixed, the partition of
is fixed, the partition of ![]() has to be
properly chosen for purposes of block addition or multiplication.
has to be
properly chosen for purposes of block addition or multiplication.
A K Lal 2007-09-12