DEFINITION 1.3.1
- A matrix
 over
over
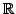 is called symmetric if
is called symmetric if
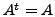 and skew-symmetric if
and skew-symmetric if
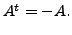
- A matrix
 is said to be orthogonal if
is said to be orthogonal if
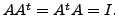
EXAMPLE 1.3.2
- Let
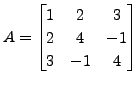 and
and
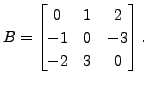 Then
Then  is a symmetric matrix and
is a symmetric matrix and
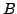 is a skew-symmetric matrix.
is a skew-symmetric matrix.
- Let
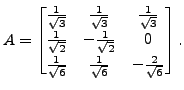 Then
Then
 is an orthogonal matrix.
is an orthogonal matrix.
- Let
![$ A=[a_{ij}]$](img20.png) be an
be an
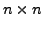 matrix with
matrix with
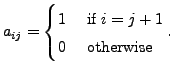 Then
Then
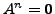 and
and
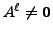 for
for
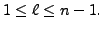 The matrices
The matrices  for which a positive integer
for which a positive integer 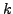 exists such that
exists such that
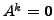 are called NILPOTENT
matrices. The least positive integer
are called NILPOTENT
matrices. The least positive integer 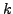 for which
for which
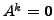 is called the ORDER OF NILPOTENCY.
is called the ORDER OF NILPOTENCY.
- Let
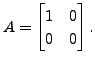 Then
Then 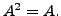 The matrices that satisfy the condition that
The matrices that satisfy the condition that 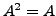 are called IDEMPOTENT
matrices.
are called IDEMPOTENT
matrices.
EXERCISE 1.3.3
- Show that for any square matrix
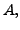
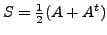 is
symmetric,
is
symmetric,
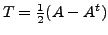 is skew-symmetric, and
is skew-symmetric, and
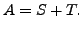
- Show that the product of two lower triangular matrices is a
lower triangular matrix. A similar statement holds for upper
triangular matrices.
- Let
 and
and 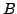 be symmetric matrices. Show that
be symmetric matrices. Show that 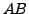 is symmetric
if and only if
is symmetric
if and only if
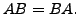
- Show that the diagonal entries of a skew-symmetric matrix
are zero.
- Let
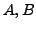 be skew-symmetric matrices with
be skew-symmetric matrices with
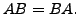 Is the matrix
Is the matrix 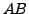 symmetric or skew-symmetric?
symmetric or skew-symmetric?
- Let
 be a symmetric matrix of order
be a symmetric matrix of order 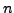 with
with
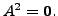 Is it necessarily true that
Is it necessarily true that
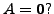
- Let
 be a nilpotent matrix. Show that there exists a matrix
be a nilpotent matrix. Show that there exists a matrix  such that
such that
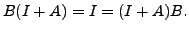
Subsections
A K Lal
2007-09-12
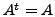 and skew-symmetric if
and skew-symmetric if
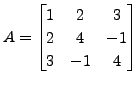 and
and
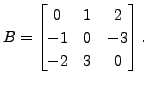 Then
Then 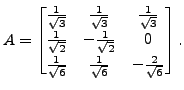 Then
Then
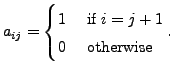 Then
Then
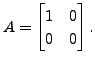 Then
Then