Next: Inverse of a Matrix Up: Operations on Matrices Previous: Operations on Matrices Contents
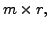 with
with
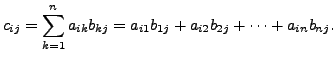
That is, if
![$ A_{m \times n} = \left[\begin{array}{cccc} & & \cdots & \\ & & \cdots & \\
a_...
...a_{i2} & \cdots & a_{in} \\ & & \cdots & \\ & & \cdots & \\
\end{array}\right]$](img96.png) and
and
![$ B_{n \times r} = \left[\begin{array}{ccc} \cdots & b_{1j} & \cdots \\
\cdots ...
... \\ \vdots & \vdots & \vdots \\
\cdots & b_{mj} & \cdots \\ \end{array}\right]$](img97.png) then
then
Observe that the product
For example, if
However, for square matrices
Part 5.
The reader is required to prove the other parts.
height6pt width 6pt depth 0pt
![]() is defined if and only if
is defined if and only if
THE
NUMBER OF COLUMNS OF
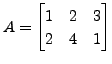 and
and
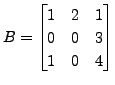 then
then
Observe the following:
![]() is defined,
the product
is defined,
the product ![]() is not defined.
is not defined.
![]() and
and ![]() of the same order, both the product
of the same order, both the product
![]() and
and ![]() are defined.
are defined.
![]() corresponds to operating on the rows of the matrix
corresponds to operating on the rows of the matrix ![]() (see 1.2.1), and
(see 1.2.1), and
![]() also corresponds to operating on the columns of the matrix
also corresponds to operating on the columns of the matrix ![]() (see 1.2.2).
(see 1.2.2).
![]() and
and ![]() are said to commute if
are said to commute if
![]()
![]() is a square matrix of order
is a square matrix of order ![]() then
then
![]() Also, a scalar matrix of order
Also, a scalar matrix of order ![]() commutes with any
square matrix of order
commutes with any
square matrix of order ![]() .
.
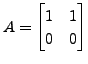 and
and
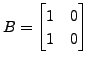 . Then check that the matrix
product
. Then check that the matrix
product 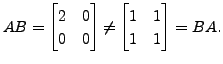
![]() and
and ![]() are so chosen that the matrix multiplications are defined.
are so chosen that the matrix multiplications are defined.
![]() That is, the matrix multiplication is associative.
That is, the matrix multiplication is associative.
![]()
![]() That is, multiplication
distributes over addition.
That is, multiplication
distributes over addition.
![]() is an
is an
![]() matrix then
matrix then
![]()
![]() of order
of order ![]() and
and
![]() we have
we have
A similar statement holds for the columns
of ![]() is
is ![]() times the first row of
times the first row of ![]()
![]() the
the
![]() row
of
row
of ![]() is
is ![]() times the
times the
![]() row of
row of ![]()
![]() when
when ![]() is multiplied on the right by
is multiplied on the right by ![]()
![]() Let
Let
![]() and
and
![]() Then
Then
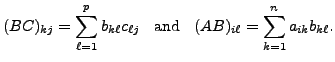
![]()
![]()
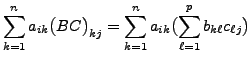
![]()
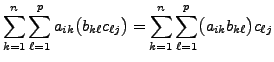
![]()
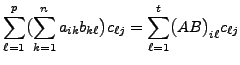
![]()
![]()
![]() For all
For all
![]() we have
we have
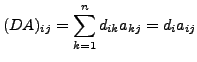
![]() whenever
whenever ![]() Hence, the required result follows.
Hence, the required result follows.
![]() and
and ![]() be two matrices. If the matrix addition
be two matrices. If the matrix addition ![]() is defined,
then prove that
is defined,
then prove that
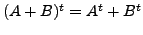 . Also, if the matrix product
. Also, if the matrix product ![]() is
defined then prove that
is
defined then prove that
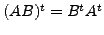 .
.
![]() and
and
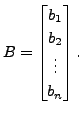 Compute the matrix products
Compute the matrix products ![]() and
and ![]()
![]() be a positive integer. Compute
be a positive integer. Compute ![]() for the following matrices:
for the following matrices:
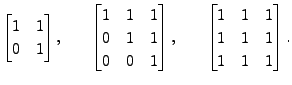
![]() and prove it by induction?
and prove it by induction?
![]() is defined. Then the product
is defined. Then the product
![]() need not be defined.
need not be defined.
![]() and
and ![]() are defined. Then
the matrices
are defined. Then
the matrices ![]() and
and ![]() can have different orders.
can have different orders.
![]() and
and ![]() are square matrices of order
are square matrices of order ![]() Then
Then ![]() and
and ![]() may or may not be equal.
may or may not be equal.