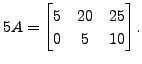DEFINITION 1.2.1 (Transpose of a Matrix)
The transpose of an
 matrix
matrix
![$ A=[a_{ij}]$](img20.png) is defined
as the
is defined
as the
 matrix
matrix
![$ B = [b_{ij}],$](img53.png) with
with
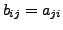 for
for
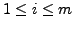 and
and
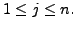 The transpose of
The transpose of  is
denoted by
is
denoted by 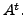
That is, by the transpose of an
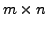 matrix
matrix 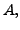 we mean a matrix
of order
we mean a matrix
of order
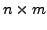 having the rows of
having the rows of  as its columns and the
columns of
as its columns and the
columns of  as its rows.
as its rows.
For example, if
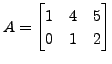 then
then
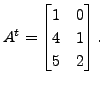
Thus, the transpose of a row
vector is a column vector and vice-versa.
THEOREM 1.2.2
For any matrix 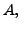
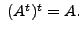
Proof.
Let
![$ A = [a_{ij}], \; A^t = [b_{ij}]$](img63.png)
and
![$ (A^t)^t = [c_{ij}].$](img64.png)
Then, the definition of transpose gives
and the
result follows.
height6pt width 6pt depth 0pt
DEFINITION 1.2.3 (Addition of Matrices)
let
![$ A=[a_{ij}]$](img20.png) and
and
![$ B= [b_{ij}]$](img21.png) be are two
be are two
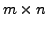 matrices. Then the sum
matrices. Then the sum 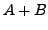 is defined to be the matrix
is defined to be the matrix
![$ C =
[c_{ij}]$](img67.png) with
with
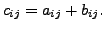
Note that, we define the sum of two matrices only when the order of
the two matrices are same.
DEFINITION 1.2.4 (Multiplying a Scalar to a Matrix)
Let
![$ A=[a_{ij}]$](img20.png) be an
be an
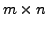 matrix.
Then for any element
matrix.
Then for any element
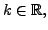 we define
we define
![$ k A = [k a_{ij}].$](img70.png)
For example, if
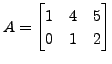 and
and 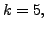 then
then
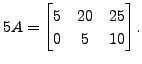
Proof.
Part
1.
Let
![$ A=[a_{ij}]$](img20.png)
and
![$ B= [b_{ij}].$](img81.png)
Then
as real numbers commute.
The reader is required to prove the other parts as all the results
follow from the properties of real numbers.
height6pt width 6pt depth 0pt
EXERCISE 1.2.6
- Suppose
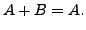 Then show that
Then show that
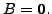
- Suppose
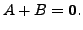 Then show that
Then show that
![$ B = (-1) A = [- a_{ij}].$](img86.png)
DEFINITION 1.2.7 (Additive Inverse)
Let  be an
be an
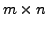 matrix.
matrix.
- Then there exists a matrix
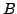 with
with
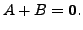 This matrix
This matrix 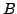 is called the additive
inverse of
is called the additive
inverse of 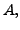 and is denoted by
and is denoted by
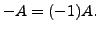
- Also, for the matrix
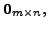
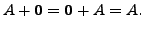 Hence, the matrix
Hence, the matrix
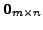 is called the additive identity.
is called the additive identity.
Subsections
A K Lal
2007-09-12
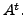
![]() matrix
matrix ![]() we mean a matrix
of order
we mean a matrix
of order
![]() having the rows of
having the rows of ![]() as its columns and the
columns of
as its columns and the
columns of ![]() as its rows.
as its rows.
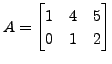 then
then
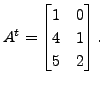
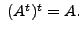
![$ A = [a_{ij}], \; A^t = [b_{ij}]$](img63.png) and
and
![$ (A^t)^t = [c_{ij}].$](img64.png) Then, the definition of transpose gives
Then, the definition of transpose gives
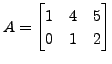 and
and