Next: Operations on Matrices Up: Definition of a Matrix Previous: Definition of a Matrix Contents
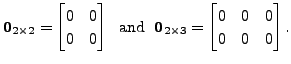
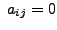 for
for 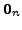 and
and
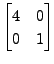 are a few diagonal matrices.
are a few diagonal matrices.
A diagonal matrix ![]() of order
of order ![]() with the diagonal entries
with the diagonal entries
![]() is denoted by
is denoted by
![]()
If ![]() for all
for all
![]() then the diagonal matrix
then the diagonal matrix
![]() is called a scalar matrix.
is called a scalar matrix.
For example,
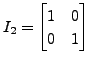 and
and
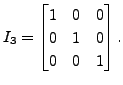
The subscript ![]() is suppressed in case the
order is clear from the context or if no confusion arises.
is suppressed in case the
order is clear from the context or if no confusion arises.
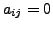 for
for
A square matrix
![]() is said to be a lower
triangular matrix if
is said to be a lower
triangular matrix if
![]() for
for ![]()
A square matrix ![]() is said to be triangular if it is an
upper or a lower triangular matrix.
is said to be triangular if it is an
upper or a lower triangular matrix.
For example
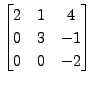 is an upper triangular matrix. An upper triangular
matrix will be represented by
is an upper triangular matrix. An upper triangular
matrix will be represented by
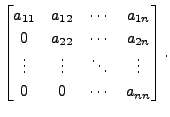
A K Lal 2007-09-12