Next: Linear System of Equations Up: Matrices Previous: Miscellaneous Exercises Contents
Here the entries of the matrix are complex numbers. All the definitions still hold. One just needs to look at the following additional definitions.
For example, Let
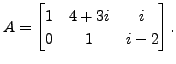 Then
Then
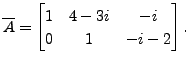
For example, Let
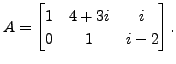 Then
Then
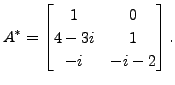
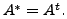
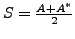 is Hermitian,
is Hermitian,
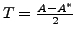 is skew-Hermitian, and
is skew-Hermitian, and
A K Lal 2007-09-12