Proofs of (i) and (ii) follow directly from the lemma 16.1.6. Thus, by the completeness property of 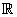 , both , both 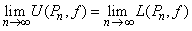 exist. That for a continuous function, both these sequences converge to a common limit, and that limit is independent of the sequence exist. That for a continuous function, both these sequences converge to a common limit, and that limit is independent of the sequence 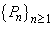 of refinement partitions of of refinement partitions of 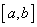 is technical, and we assume this. is technical, and we assume this.
|