For  , each , each  is the area of the rectangle with base is the area of the rectangle with base  and height and height  . The number . The number  is the sum of the areas of all such rectangles. These rectangles cover of the region is the sum of the areas of all such rectangles. These rectangles cover of the region  . Similarly, each . Similarly, each  and and  is the area of the rectangle with base is the area of the rectangle with base  and height and height  . The number . The number  is the sum of all these rectangles which try to fill up the region is the sum of all these rectangles which try to fill up the region  . The sum . The sum  under estimates the Ďarea' of under estimates the Ďarea' of  and and  over estimates the area of over estimates the area of  , i.e., , i.e.,
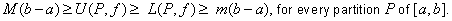
|