Note that for every partition 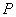 , the sum , the sum 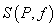 depends not only on the partition depends not only on the partition 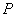 , but also on the choice of points , but also on the choice of points 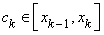 . However, for every partition . However, for every partition 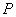 , the following holds: , the following holds:
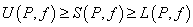 . .
We hope that as we make 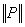 smaller and smaller, the Riemann sum smaller and smaller, the Riemann sum 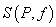 will approximate the required area better and better. This actually does happen for integrable functions. In fact, we have the following: will approximate the required area better and better. This actually does happen for integrable functions. In fact, we have the following:
|