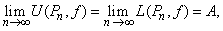
then for every sequences of refinement partitions, the upper and the lower sum sequences converge to the same limit, namely, 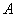 .Thus, theorem 16.1.7 (iii) says the following: .Thus, theorem 16.1.7 (iii) says the following:
 Every continuous function Every continuous function 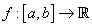 is integrable. is integrable.
In fact, if  is a bounded function such that is a bounded function such that 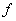 has only finite number of discontinuities, say at has only finite number of discontinuities, say at 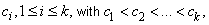 then it can be shown that then it can be shown that 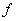 is integrable on is integrable on 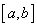 and and
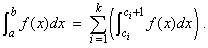 |