(iv) If 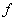 and and 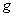 are integrable, then are integrable, then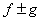 are integrable and are integrable and
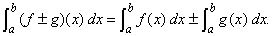
(v) If 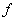 and and 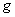 are integrable and are integrable and 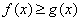 for all for all 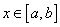 , then , then
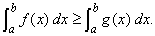
(vi) If 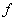 is integrable on is integrable on 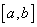 , then , then 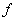 is integrable over every interval is integrable over every interval 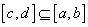 and and
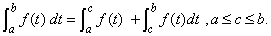
This is called the additive property of the integral.
(we define 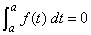 for every for every 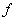 ). ).
(vii)If 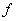 and and 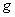 are integrable, then are integrable, then 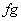 is also integrable. is also integrable.
|