| |
Electric displacement vector 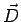 helps us to calculate fields in the presence of a dielectric. This is possible only if a relationship between helps us to calculate fields in the presence of a dielectric. This is possible only if a relationship between 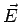 and and 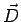 is known. is known. |
| |
For a weak to moderate field strength, the electric polarization 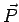 is found to be directly proportional to the external electric field is found to be directly proportional to the external electric field 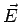 . We define Electric Susceptibility . We define Electric Susceptibility 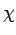 through through |
| |
where 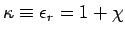 is called the relative permittivity or the dielectric constant and is called the relative permittivity or the dielectric constant and 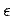 is the permittivity of the medium. Using differential form of Gauss's law for is the permittivity of the medium. Using differential form of Gauss's law for 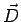 , we get , we get |
| |
Thus the electric field produced in the medium has the same form as that in free space, except that the field strength is reduced by a factor equal to the dielectric constant 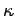 . |