| |
The first integral can be converted to a surface integral using the divergence theorem giving, |
 |
|
| |
The first term is the potential that one would expect for a surface charge density 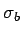 where where |
| |
|
| |
where 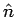 is the unit vector along outward normal to the surface. The second term is the potential due to a volume charge density is the unit vector along outward normal to the surface. The second term is the potential due to a volume charge density 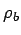 given by given by |
| |
|
| |
The potential due to the dielectric is, therefore, given by |
| |
|
| |
and the electric field |
| |
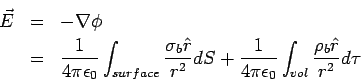 |
| |
|
|