If the atoms are in thermal equilibrium with the surrounding at a temperature 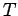 , the relative population in the two levels are given by Boltzmann distribution , the relative population in the two levels are given by Boltzmann distribution
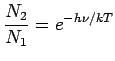
This equation shows that as the temperature increases, the population of excited states increase. However, the population of an excited state always lies lower than the population of the ground state, under equilibrium condition. For large energy gaps such that 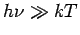 , the ratio above is close to zero so that very few of the atoms are in the upper energy state. , the ratio above is close to zero so that very few of the atoms are in the upper energy state. |