where 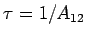 gives the average gives the average 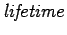 of an atom in the excited level before the atom returns to the ground state. Thus the spontaneous emission depends on the lefetime of the atom in the excited state. The process is statistical and the emitted quanta bear no phase relationship with one another, i.e. the emission is incoherent . of an atom in the excited level before the atom returns to the ground state. Thus the spontaneous emission depends on the lefetime of the atom in the excited state. The process is statistical and the emitted quanta bear no phase relationship with one another, i.e. the emission is incoherent .
- Stimulated Emission - Stimulated or induced emission depends on the number of atoms in the excited level as well as on the energy density of the incident radiation. If
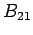 be the transition be the transition probability per unit time per unit energy density of radiation, the rate of decrease of the population of the excited state is be the transition be the transition probability per unit time per unit energy density of radiation, the rate of decrease of the population of the excited state is 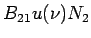 . .
The rate equation for the population of the upper level is
![$\displaystyle \frac{dN_2}{dt} = B_{12}u(\nu)N_1 - [A_{21}+B_{21}u(\nu)]N_2$](../fig/math-images/math_clip_image053.gif)
Since 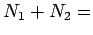 constant, constant,
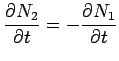
|