Using the Boltzmann facor 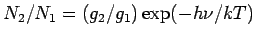 , and simplifying, we get , and simplifying, we get
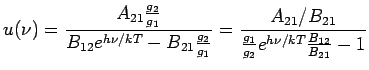
If we regard the matter to be a blackbody and compare the above expression for the energy density with the corresponding energy density expression derived for the blackbody radiation, viz.,
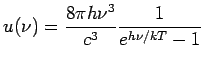
we get
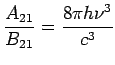
and
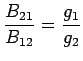
The last equation shows that n the absence of degeneracy, the probability of stimulated emission is equal to that of absorption. In view of this we replace the two coefficients by a single coefficient 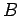 and term them as and term them as 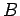 - coefficient. The spontaneous emission coefficient will be called the - coefficient. The spontaneous emission coefficient will be called the 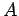 - coefficient. - coefficient. |