The distribution of atoms in the two energy levels will change by absorption or emission of radiation. Einstein introduced three empirical coefficients to quantify the change of population of the two levels.
- Absorption - If
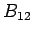 is the probability (per unit time) of absorption of radiation, the population of the upper level increases. The rate is clearly proportional to the population of atoms in the lower level and to the energy density is the probability (per unit time) of absorption of radiation, the population of the upper level increases. The rate is clearly proportional to the population of atoms in the lower level and to the energy density 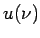 of radiation in the system. Thus the rate of increase of population of the excited state is given by of radiation in the system. Thus the rate of increase of population of the excited state is given by
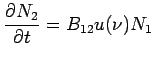
where 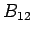 is a constant of proportionality with dimensions m is a constant of proportionality with dimensions m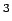 /s /s 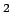 -J. -J.
- Spontaneous Emission - The population of the upper level will decrease due to spontaneous transition to the lower level with emission of radiation. The rate of emission will depend on the population of the upper level. If
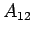 is the probability that an atom in the excited state will spontaneously decay to the ground state, is the probability that an atom in the excited state will spontaneously decay to the ground state,
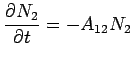
The equation above has the solution
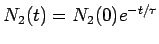 |