2. PID Controller for SISO systems
PID controller is commonly used for SISO systems. Figure 3.4.2 shows the basic blocks of a SISO system. It has single input and single output. It has a controller which controls the operation of a process based on the feedback received.
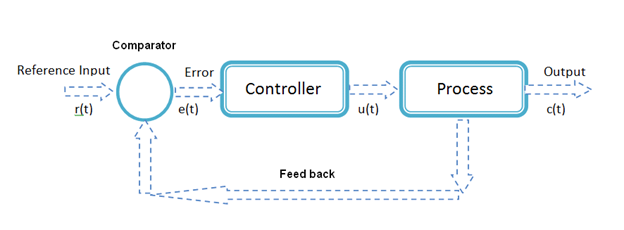
Figure 3.4.2 A SISO system.
For a PID controller, the output can be expressed in terms of input as follows:
 |
(3.4.1.) |
And the transfer function of PID controller can be written as,
 |
(3.4.2.) |
Where
Kp → Proportional Gain
τd → Derivative Time
τi → Integral Time
PID controller consists of Proportional, Integrator and Differentiator Controllers which can be understood by considering a first order system SISO whose transfer function can be written as,
 |
(3.4.3.) |
Now let us study the Proportional, Integrator and Differentiator Controllers one by one and then adding them together as PID controller.
2.1 Proportional Controller (P – Controller)
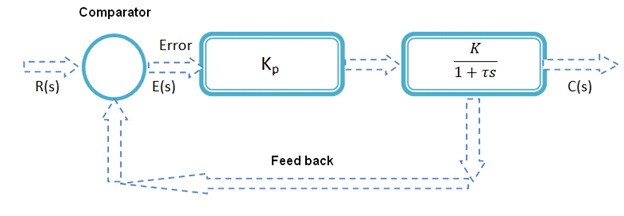
Figure 3.4.3 Proportional controller
The proportional controller gives an output value that is proportional to the error value with a gain value of Kp. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain constant (Eq. 3.4.1). Figure 3.4.3 shows the schematic of a proportional controller for a closed loop control system, the transfer function can be written as,
 |
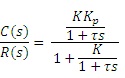(3.4.4.) |
 |
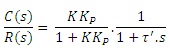(3.4.5.) |
Thus unit step response for Proportional Controller will be,
 |
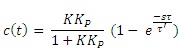(3.4.6.) |
Effect of adding Proportional Controller in the system:
On adding a proportional controller in system, Time response of system improves by a factor of 
. Also on adding proportional controller, steady state offset arises between desired response and output response as shown in figure 3.4.4.
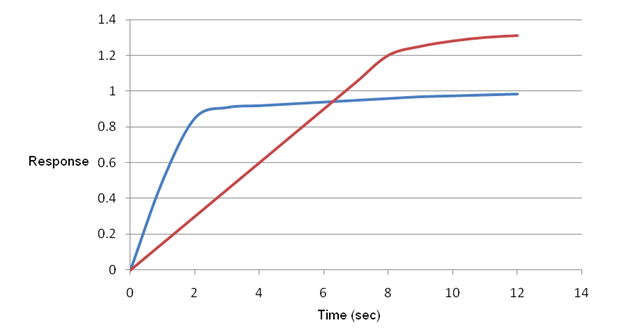
Figure 3.4.4 System response with and without P-controller