 |
(5.67) |
and
 |
(5.68) |
which can be rearranged in matrix form as
 |
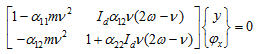(5.69) |
Equations (5.69) are homogeneous equations in y and φx, on putting determinant of the matrix equal to zero, we get the frequency equation as
 |
(5.70) |
Equation contain seven system parameters: ω, v, m, Id, 
, 
, and 
, which makes a good understanding of the solution very difficult. It should be kept in mind that above frequency equation represents a large class of single-mass rotor system and depending upon boundary conditions (e.g., the simply supported, cantilever, fixed-fixed, over-hang, etc.) only the influence coefficient expressions (i.e., (5.67)) would change. It is worthwhile to diminish the number of parameters as much as possible by the dimensional analysis. Introducing four new variables
 |
(5.71) |
With this new four non-dimensional variables, equation becomes
 |
(5.72) |
Equation (5.72) is the fourth degree polynomial in 
, so for a given 
, carrying a given disc μ, and rotating at certain speed 
, there will be four natural frequencies of the whirl.
Case I: For a point mass of the disc, i.e., Id = 0 or μ = 0. Multiply equation (5.72) by μ and on substituting μ = 0, we get
 |
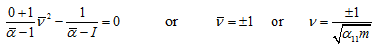(5.73) |
Since = 1/k in the usual natural notation, we have the expression for the natural frequency of the whirl as
 |
(5.74) |
This result is very much familiar.
Case II: = 0, i.e., no elastic coupling. For this case a force causes a linear deflection only without an angular deflection φx, while a moment causes an angular deflection φx only without linear deflection y. For a shaft with simple supports and a disc at the mid-span, such a case is possible as shown in Figure 5.29.
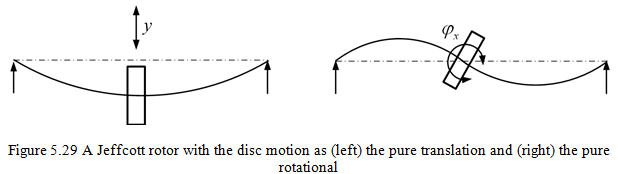
Equation (5.72) reduces to
 |
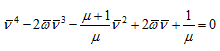(5.75) |
Equation (5.75) can be written as
 |
(5.76) |
Equation (5.76) gives
 |
(5.77) |
and
 |
(5.78) |
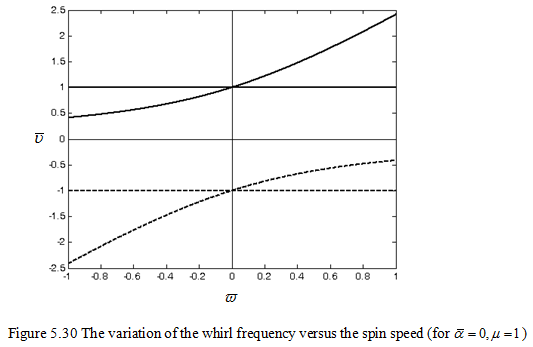
The non-dimensional frequency is plotted against the speed for the numerical value μ = 1 as shown in Figure 5.30. For = 0 from the first and second solutions, i.e. equation (5.77), we have = ±1, which is the natural frequency related to the up and down motions without any tilting. For = 0 from the third and fourth solutions, i.e. equation (5.78), we have 
and since μ = 1, hence = ±1. This is the natural frequency related to the precessional motion, i.e. wobbling without up and down motions. From equation (5.78), it can be seen that for the present case the second forward critical speed (for 
) would not be feasible and only the second backward critical speed (for ) would be 
.
The disc effect μ is so chosen or dimensioned such that the natural frequency of the linear up and down motions is the same as the natural frequency of the wobbling (tilting) without up and down motions at zero speed, i.e. = 0 (see in Figure 5.30). It should be noted that these kind of uncoupling of the linear and angular motions is a special case with = 0 and in general such uncoupling of motions is not possible and for such systems all natural frequencies both the linear and angular motions would be present with different relative magnitudes and directions. From equation (5.71), we have
 |
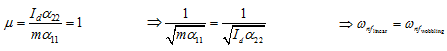(5.79) |
Figure 5.30 shows that there are four natural frequencies at any given speed. For positive value of , it could be seen that corresponding to the linear up and down motion, the natural whirl frequency remains constant. Whereas, for tilting motion corresponding to the forward whirl it increases and for backward whirl it decreases. For -, the frequency curve is symmetric with respect to = 0 line, which means the natural frequency does not depend upon the direction of rotation of the symmetric rotor. For the zero speed the four natural frequencies is reduced to two = ±1, which is really one frequency only because = +1 corresponding to the forward whirl and = -1 corresponding to the backward whirl and the non-rotating shaft can not distinguish the forward and backward whirls.
Case III: Now the frequency equation (5.72) is plotted, which is for the general motion when the disc has both the linear and angular motions, simultaneously.
Taking a case of cantilever shaft with a disc (it should be noted that any other boundary conditions can be taken at this stage), for which the elastic coupling can be obtained as
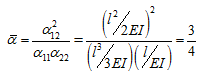and taking again μ = 1.
For = ¾ and m = 1, equation (5.72) becomes
 |
(5.80) |
Equation (5.80) is the fourth degree polynomial in with four roots = ƒ(). It can be solved in two ways (i) Take a value of and solve fourth degree polynomial equation in , or (ii) Take a value of and solve a linear equation in , i.e. equation can be rearranged as
 |
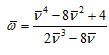(5.81) |