5.5 Asynchronous General Motion
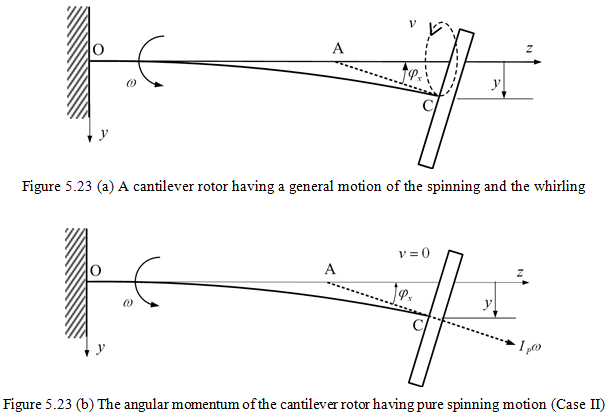
In the previous critical speed analysis of the cantilever rotor in Section 5.3, the rotor was whirling (the whirling is defined as a circular motion of the deflected shaft centre line about its undeflected position with small amplitude) and spinning at the same angular speed and in the same direction (i.e., the synchronous whirl case). So in that analysis we concentrated more on the critical speed determination rather than obtaining variation of whirl frequency with spin speed of the shaft for a general motion. In fact we attempted a special case for which the spin speed was equal to whirl frequency. Cases have been observed where whirling and the spinning occur at different frequencies and sometimes in opposite directions as described in the previous section (Section 5.4), in which the analysis was for only the pure rotational motion. The aim of the present section is to calculate natural whirling frequencies, v, of a shaft with a single disc on it at any speed of rotation, ω, in most general manners as shown in Figure 5.23(a), where ω is the shaft spin speed about deflected centerline and n is the shaft whirling frequency about undeformed position OA. Since a general motion of the disc is very difficult to visualize hence the following three cases have been considered that is relatively easier to visualize, and the final motion will be superposition of some of these cases (i.e., cases I and II).
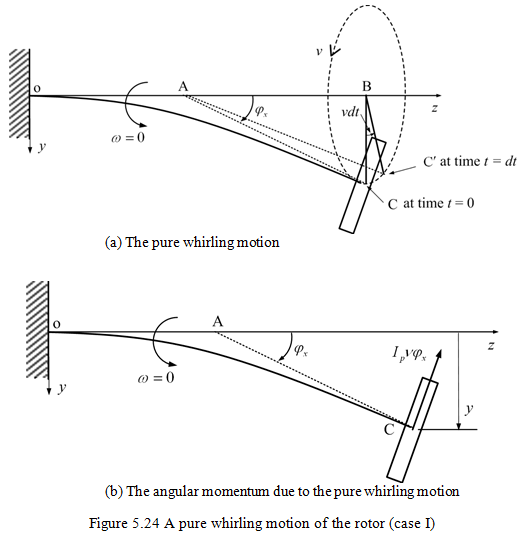
Case I: v = v0 with ω = 0 (Pure whirling motion)
The shaft does not spin about its deflected centerline, but deflected centerline OC whirls with v0 about bearing centre line OA.
Case II: v = 0 with ω = ω0 (Pure spinning motion)
The shaft is in the deflected position OC, and it spins with ω0 about the deflected centerline OC.
Case III: v = ω (Synchronous whirling and spinning motions)
The shaft fiber in tension remains in tension, and similarly shaft fiber in compression remains in compression, i.e. the synchronous whirl. This analysis directly gives critical speeds. It has already been discussed in detail in Section 5.3 and it will not be discussed here again.
With this combined v and ω motions (Cases I and II), our first aim would be to obtain its angular momentum. For case II when it does not whirl, but only spins, the angular momentum is equal to Ipω (along AC as shown in Figure 5.23b) where Ip is the polar moment of inertia of the disc.
Pure whirling motion