Isometric view of some standard shapes

1.Square

Consider a square ABCD with a 30 mm side shown in Fig.  If the square lies in the vertical plane, it will appear as a rhombus with a 30 mm side in isometric view as shown in Fig. (a) or (b), depending on its orientation, i.e., right-hand vertical face or left-hand vertical face. If the square lies in the horizontal plane (like the top face of a cube), it will appear as in Fig.(c). The sides AB and AD, both, are inclined to the horizontal reference line at 30°.

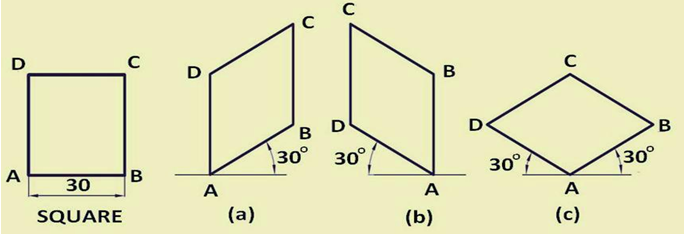
Figure 10. Isometric views of a square.

2.Rectangle

A rectangle appears as a parallelogram in isometric view as shown in figure 11.. Three versions are possible depending on the orientation of the rectangle, i.e., right-hand vertical face, left-hand vertical face or horizontal face.

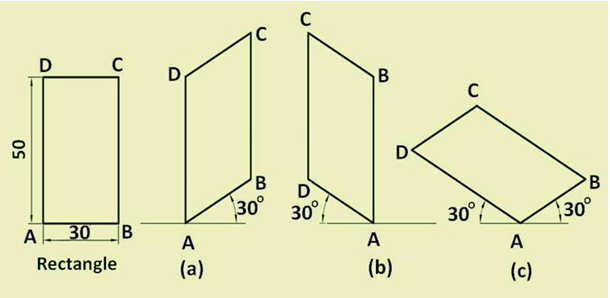
Figure 11. Isometric views of a rectangle.

3.Triangle

A triangle of any type can be easily obtained in isometric view as explained below. First enclose the triangle in rectangle ABCD. Obtain parallelogram ABCD of the rectangle as shown in Fig. 12(a) or (b) or (c). Then locate point 1 in the parallelogram such that C–1 in the parallelogram is equal to C–1 in the rectangle. A–B–1 represents the isometric view of the triangle.

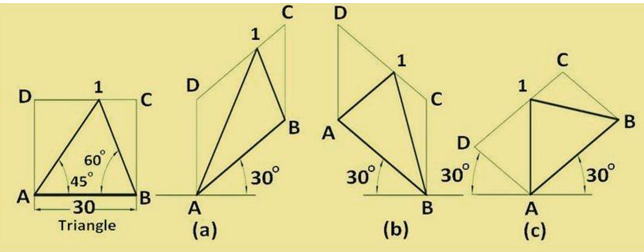
Figure 12. Method of obtaining the isometric views of a triangle.