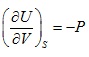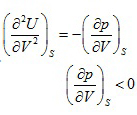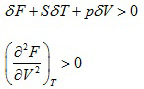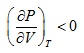Also

(2.130)

Thus,

(2.131)   (2.132)

Hence the adiabatic bulk modulus must be negative. Again

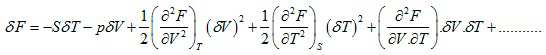
For stability

(2.133) (2.134)

Again

(2.135) (2.136) (2.137)

Which is known as the condition of mechanical stability. The isothermal bulk modulus must also be negative.

Example 5

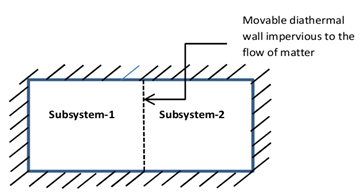
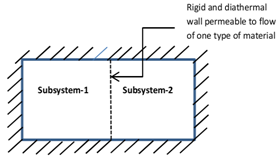
Establish the condition of equilibrium of a closed composite system consisting of two simple systems (a) separated by a movable diathermal wall that is impervious to the flow of matter and (b) If the walls were rigid and diathermal, permeable to one type of material, and impermeable to all others, state the condition of equilibrium of the composite system.

Solution
(a) For the composite system, as shown in Fig. A

Fig. A Two subsystems with a movable diathermal wall impervious to the flow of matter

The values of would change in such a way as to maximize the value of entropy. Therefore, when the equilibrium condition is achieved

dS = 0

for the whole system. Since

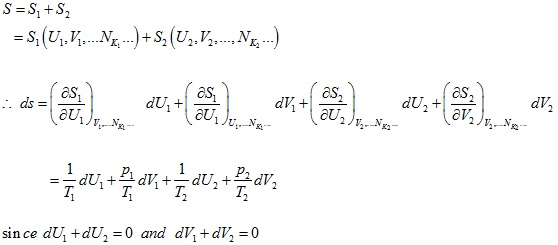
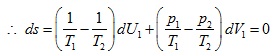
Since the expression must vanish for arbitrary and independent values of dU 1 and dV 2

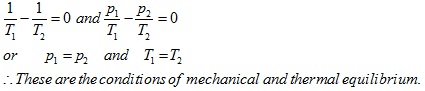
(b) we will consider the equilibrium state of two simple subsystems connected by a rigid and diathermal wall, permeable to one type of material (N₁) and impermeable to all others (N₂,N₃, ..... N_r) (Fig B). We thus seek the equilibrium values of U₁ and of U₂ , and of N_1-1 and N_1-2 (i.e. material N₁ in subsystems 1 and 2 respectively.)

Fig. B Two subsystems with a rigid diathermal wall permeable to the flow of one type of matter and impermeable to all other type of materials.

At equilibrium, an infinitesimal change in entropy is zero

dS = 0

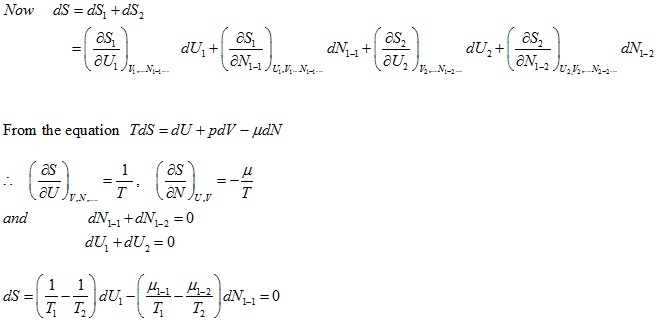
As dS must vanish for arbitrary values of both dU₁ and dN_1-1
T₁ = T₂
μ_1-1 = μ_1-2
Which are the conditions of thermal and chemical equilibrium.