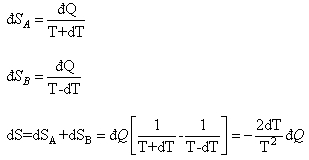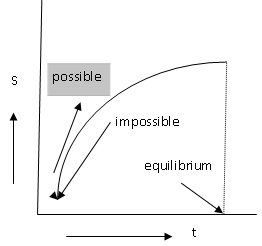
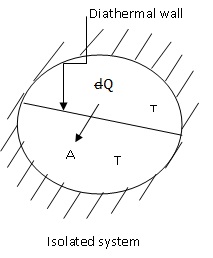
A system is said to be in a state of stable equilibrium if, when the state is perturbed, the system returns to its original state. A system is not in equilibrium if there is a spontaneous change in the state. If there is a spontaneous change in the system, the entropy of the system increases and reaches a maximum when the equilibrium condition is reached (fig. 2.11). Both A and B (fig. 2.12) are assumed to be at the same temperature T. Let there be some spontaneous change; the temperature of A rises to T + dT, and that of B decreases to T - dT. For simplicity, let the heat capacities of the bodies be the same, so that difference of temperature dT is same for the both the systems A and B. If 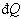is the heat interaction involved, then the entropy change

Fig. 2.11

Fig. 2.12

(2.107)   (2.108)

so there is a decrease in entropy for the isolated system with A and B together. It is thus clear that the variation in temperature dT cannot take place. The system, therefore, exists in a stable equilibrium condition. Perturbation of the state produces an absurd situation and the system must revert to the original stable state. It may be observed:

if for all the possible variations in state of the isolated, there is a negative change in entropy, then the state is in stable equilibrium.

(2.109)

Similarly

(2.110)