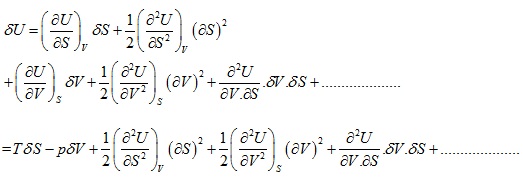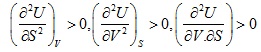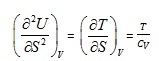Again
|
(2.119) |
When ![]() at equilibrium
at equilibrium
T1 = T2, p1 = p2 |
(2.120) |
Conditions of stability
At equilibrium,
|
(2.121) |
these are necessary but not sufficient conditions for equilibrium. To prove that S is a maximum, and G or F a minimum, it must satisfy ![]()
If the system is perturbed, and for any infinitesimal change of the system
|
(2.122) |
It represents the stability of the system. The system must revert to the original state.
For a spontaneous change, from Equation
|
(2.123) |
For stability
|
(2.124) |
Let us choose U=U(S, V) and represents ![]() in powers of
in powers of
|
(2.126) |
The third order and higher order terms are neglected.
Since ![]() it must satisfy the condition given bellow
it must satisfy the condition given bellow
|
(2.127) |
These inequalities indicate how to signs of some important physical quantities become for a system to be stable.
Since 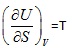
|
(2.128) |
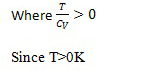
|
(2.129) |
Eq (2.129) is the condition for thermal stability.
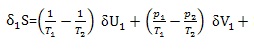 Second order terms
Second order terms