- Show that the sphere
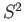 retracts onto one of its longitudes. If
retracts onto one of its longitudes. If  is the space obtained from
is the space obtained from 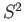 by
taking its union with a diameter, there is a surjective group homomorphism
by
taking its union with a diameter, there is a surjective group homomorphism
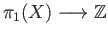 .
.
- Prove that
 is a retract of
is a retract of  if and only if every space
if and only if every space  ,
every continuous map
,
every continuous map
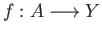 has a continuous extension
has a continuous extension
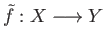 .
.
- Show that the fundamental group respects arbitrary products.
- Construct a retraction from
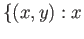 or
or  is an integer
is an integer onto the boundary of
onto the boundary of 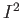 .
.
- Show that every homeomorphism of
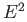 onto itself must map the boundary to the boundary.
onto itself must map the boundary to the boundary.
- Given that there exists a functor
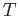 from the category
from the category  to the category
to the category
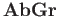 such that
such that
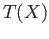 is the trivial group for every convex subset
is the trivial group for every convex subset  of a Euclidean space and
of a Euclidean space and 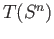 is a non-trivial group,
prove that
is a non-trivial group,
prove that  is not a retract of the closed unit ball in
is not a retract of the closed unit ball in
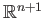 .
.
in
Lecture X - Brouwer's Theorem and its Applications.
in
In this lecture we shall prove the Brouwer's fixed point theorem and deduce some of its consequences
such as the Perron-Frobenius' theorem.
The one dimensional Brouwer's theorem follows from the intermediate value property as is
indicated in the exercises of lecture 3.
We also include a proof of the fact that the spheres  have trivial fundamental group
when
have trivial fundamental group
when 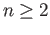 . This result has been included here to demonstrate why the fundamental group is insufficient to
prove the Brouwer's fixed point theorem in dimension three or higher.
. This result has been included here to demonstrate why the fundamental group is insufficient to
prove the Brouwer's fixed point theorem in dimension three or higher.
We begin by defining the fixed point property for a space. Here we require the fixed point property to hold for all continuous functions
of the space into itself.
Note that in analysis the spaces considered are somewhat special
and so are the maps whose fixed point property are sought. A classic example of such a restricted fixed point theorem is the
Banach's fixed point theorem.
Subsections
nisha
2012-03-20