Let  be a
be a 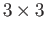 matrix with strictly positive real entries and
matrix with strictly positive real entries and 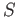 be the part of the sphere
be the part of the sphere
Then 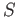 is homeomorphic to the closed unit disc in the plane (why?)
and so has the fixed point property. If
is homeomorphic to the closed unit disc in the plane (why?)
and so has the fixed point property. If 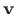 is any
unit vector with non-negative entries then the entries of
is any
unit vector with non-negative entries then the entries of 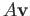 are non-negative and
at-least one of the entries must be positive. Hence
the map
are non-negative and
at-least one of the entries must be positive. Hence
the map
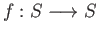 given by
given by
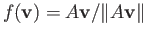 is continuous. By Brouwer's fixed point theorem,
is continuous. By Brouwer's fixed point theorem,  has a fixed point
has a fixed point 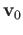 which means
which means
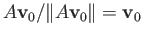 from which we infer that
from which we infer that
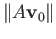 is an eigen-value of
is an eigen-value of  and this must be positive.
and this must be positive.
nisha
2012-03-20