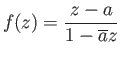Next: Theorem 10.2 (Brouwer's fixed Up: Exercises Previous: Proof:
(ii) A non-trivial topological group does not have the fixed point property.
(iii) The space
![]() has the fixed point property but we are not yet ready to prove this.
has the fixed point property but we are not yet ready to prove this.
(iv) The open unit disc
![]() does not have the fixed point property.
For if
does not have the fixed point property.
For if ![]() is a non-zero
complex number with
is a non-zero
complex number with ![]() then the map
then the map
![]() given by
given by