Let us choose a base point
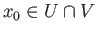 and
and  be an arbitrary loop in
be an arbitrary loop in
 based at
based at  . The open cover
. The open cover
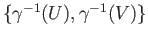 of
of ![$ [0, 1]$](img13.png) has a Lebesgue number
has a Lebesgue number 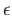 . Choose a partition
. Choose a partition
such that the length of each sub-interval is less than 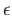 . Then
. Then  maps each
maps each
![$ [t_j, t_{j+1}]$](img866.png) into
into  or
or  . If
. If  maps
two adjacent intervals into
maps
two adjacent intervals into  or into
or into  then drop the abutting point of the two intervals thereby coarsening the partition. Thus
may arrange it such that for each
then drop the abutting point of the two intervals thereby coarsening the partition. Thus
may arrange it such that for each
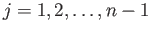 , the point
, the point
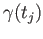 lies in
lies in 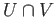 . We now
choose a path
. We now
choose a path 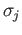 joining
joining  and
and
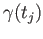 such that
the image of
such that
the image of 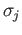 lies entirely in
lies entirely in
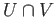 .
This is possible since
.
This is possible since 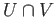 is path connected and
is path connected and
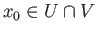 . Also let
. Also let 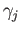 denote the restriction of
denote the restriction of  to the
sub-interval
to the
sub-interval
![$ [t_{j-1}, t_j]$](img871.png) (
(
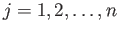 ). We may reparametrize
). We may reparametrize 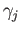 (retaining the name) so that its domain is
(retaining the name) so that its domain is ![$ [0, 1]$](img13.png) . Now
. Now
Now each of the loops
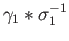 ,
,
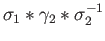 ,
,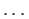 ,
,
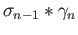 based at
based at  lies in one of the simply connected open sets
lies in one of the simply connected open sets  or
or  and so each of them is
homotopic to the constant loop via a homotopy
and so each of them is
homotopic to the constant loop via a homotopy 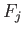 . These homotopies
. These homotopies 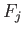 may be juxtaposed to provide a homotopy between
may be juxtaposed to provide a homotopy between
and the constant loop. The proof is complete.
nisha
2012-03-20