2.2 Theorm of Duality

The pair (A,B) is controllable if and only if the pair (A^T,B^T) is observable.

Exercise: Prove the theorem of duality.

3. Loss of controllability or observability due to pole-zero cancellation

We have already seen through an example that a system becomes uncontrollable when one of the modes is cancelled. Let us take another example.

Example:

The controllability matrix

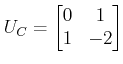
$\displaystyle U_C= \begin{bmatrix}0 & 1 \\ 1 & -2 \end{bmatrix}$

implies that the state model is controllable. On the other hand, the observability matrix

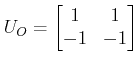
$\displaystyle U_O= \begin{bmatrix}1 & 1 \\ -1 & -1 \end{bmatrix}$

has a rank 1 which implies that the state model is unobservable. Now, if we take a different set of state variables so that, $\bar x_1(k) = y(k)$ , then the state variable model will be:

Lets us take $\bar x_2(k) = y(k+1) - u(k)$ . The new state variable model is:

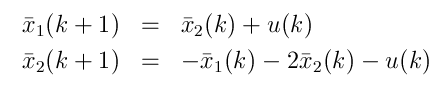
which implies $\displaystyle \bar A = \begin{bmatrix}0 & 1 \\ -1 & -2 \end{bmatrix}, \;\;\; \bar B = \begin{bmatrix}1\\ - 1\end{bmatrix}, \;\;\; C= [1 \;\;\; 0]$