1.2 Controllability to the origin and Reachability

There exist three different definitions of controllability in the literature:

1. Input transfers any state to any state. This definition is adopted in this course.

2. Input transfers any state to zero state. This is called controllability to the origin.

3. Input transfers zero state to any state. This is referred as controllability from the origin or reachability.

Above three definitions are equivalent for continuous time system. For discrete time systems definitions (1) and (3) are equivalent but not the second one.

Example: Consider the system $\boldsymbol{x}(k+1)=A\boldsymbol{x}(k)+Bu(k)$ , . where

$\displaystyle A=\begin{bmatrix}-2 & 1 \\ 1 & -2 \end{bmatrix},\quad B=\begin{bmatrix}1\\ 1\end{bmatrix} \textrm{ and }C=[ 0\;\; 1]$

Show if the system is controllable. Find the transfer function $\dfrac{Y(z)}{U(z)}$ . Can you see any connection between controllability and the transfer function?
Solution: The controllability matrix is given by

$\displaystyle U=[B\;\; AB]=\begin{bmatrix}1 & -1 \\ 1 & -1 \end{bmatrix}$

Its determinant $\Vert U\Vert=0 \Rightarrow U$ has a rank 1 which is less than the order of the matrix, i.e., 2. Thus the system is not controllable. The transfer function

Although state model is of order 2, the transfer function has order 1. The eigenvalues of A are $\lambda_1=-1$ and $\lambda_2=-3$ . This implies that the transfer function is associated with pole-zero cancellation for the pole at -3. Since one of the dynamic modes is cancelled, the system became uncontrollable.

2 Observability

Definition 2 The state model (1) (or the pair (A,C) ) is said to be observable if any initial state x(0) can be uniquely determined from the knowldge of output y(k) and input sequence u(k), for $k=0,1,2,\cdots, N$ , where N is some finite time. Otherwise the state model (1) is unobservable.

2.1 Theorems on observability

1. The state model (1) or the pair (A,C) is observable if and only if the $np\times n$ observability matrix

has rank n, i.e., full column rank.

2. The state model (1) is observable if the $n\times n$ observability grammian matrix

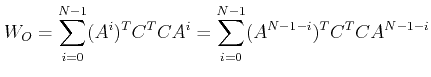$\displaystyle W_O=\sum_{i=0}^{N-1} (A^i)^T C^TC A^i=\sum_{i=0}^{N-1}( A^{N-1-i})^T C^TC A^{N-1-i}$

is nonsingular for any nonzero finite N.

3. If the state model is in observable canonical form then the system is observable.

4. When A has distinct eigenvalues and in Jordan/Diagonal canonical form, the state model is observable if and only if none of the columns of C contain zeros.

5. When A has multiple order eigenvalues and in Jordan canonical form, then the state model is observable if and only if

i. each Jordan block corresponds to one distinct eigenvalue and

ii. the elements of C that correspond to first column of each Jordan block are not all zero.