Controllability and observability are two important properties of state models which are to be studied prior to designing a controller.

Controllability deals with the possibility of forcing the system to a particular state by application of a control input. If a state is uncontrollable then no input will be able to control that state. On the other hand whether or not the initial states can be observed from the output is determined using observability property. Thus if a state is not observable then the controller will not be able to determine its behavior from the system output and hence not be able to use that state to stabilize the system.

1. Controllability

Before going to any details, we would first formally define controllability. Consider a dynamical system

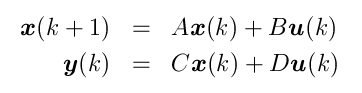(1)

where $A \in R^{n\times n}$ , $B \in R^{n\times m}$ , $C \in R^{p\times n}$ , $D \in R^{p\times m}$ .

Definition 1 The state equation (1) (or the pair (A,B) ) is said to be completey state controllable or simply controllable if for any initial state x(0) and any final state x(N), there exists an input sequence , $k=0,1,2,\cdots, N$ , which transfers x(0) to x(N) for some finite N. Otherwise the state equation (1) is uncontrollable.

Definition 2 Complete Output Controllability: The system given in equation (1) is said to be completely output controllable or simply output controllable if any final output $\boldsymbol{y}(N)$ can be reached from any initial state $\boldsymbol{x}(0)$ by applying an unconstrained input sequence $\boldsymbol{u}(k)$ , $k=0,1,2,\cdots, N$ , for some finite . Otherwise (1) is not output controllable.

1.1 Theorems on controllability

1. The state equation (1) or the pair (A,B) is controllable if and only if the $n\times nm$ controllability matrix

$\displaystyle U_C=\left[ B \;\;\;AB\;\;\; A^2B\;\;\; ......\;\;\;A^{n-1}B\right]$

has rank n, i.e., full row rank.

2. The state equation (1) is controllable if the $n\times n$ controllability grammian matrix

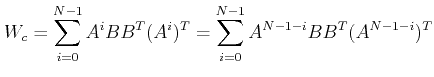$\displaystyle W_c=\sum_{i=0}^{N-1} A^i BB^T (A^i)^T=\sum_{i=0}^{N-1} A^{N-1-i} BB^T (A^{N-1-i})^T$

is nonsingular for any nonzero finite N.

3. If the system has a single input and the state model is in controllable canonical form then the system is controllable.

4. When A has distinct eigenvalues and in Jordan/Diagonal canonical form the state model is controllable if and only if all the rows of B are nonzero.

5. When A has multiple order eigenvalues and in Jordan canonical form, then the state model is controllable if and only if

i. each Jordan block corresponds to one distinct eigenvalue and

ii. the elements of B that correspond to last row of each Jordan block are not all zero.

Output Controllability: The system in equation (1) is completely output controllable if and only if the $p\times (n+1)m$ output controllability matrix

$\displaystyle U_{OC}=\left[ D \;\;\;CB\;\;\; CAB \;\;\; CA^2B\;\;\; ......\;\;\;CA^{n-1}B\right]$

has rank , i.e., full row rank.