To show that the output response is indeed deadbeat, we derive the z-transform of w(t) as $\displaystyle W(z) = 2z^{ - 1}$
Thus c(t) will actually reach its steady state in two sampling periods with no inter sample ripples which is shown in Figure 3.

Figure 3: Ripple free deadbeat response for Example 1

Example 2: Consider the plant transfer function as

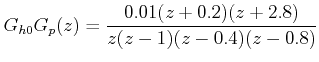
$\displaystyle G_{h0} G_p (z) = \frac{{0.01(z+0.2)(z + 2.8)}}{{z(z - 1)(z-0.4)(z - 0.8)}}$

If we apply the condition that zeros of $G_{h0} G_p (z)$ at z = - 0.2 and z = - 2.8 should not be canceled by D_c(z) , then

$\displaystyle M(z) = (1 + 0.2z^{ - 1} )(1+2.8z^{-1})m_1 z^{ - 2}$ $\displaystyle 1 - M(z) = (1 - z^{ - 1} )(1 + a_1 z^{ - 1} +a_2z^{-2}+a_3z^{-3})$

While considering M(z) and 1- M(z), following points should be kept in mind

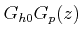1. M(z) should contain all the zeros of $G_{h0} G_p (z)$ .

2. The number of poles over zeros of M(z) should be at least equal to that of $G_{h0} G_p (z)$ which is 2 in this case.

3. 1- M(z) must include the term 1- z ^-1.

4. The orders of M(z) and 1- M(z) should be same and should equal the number of unknown coefficients.

Solving for the coefficients of M(z) and 1- M(z) , we get