One should note that poles on or outside the unit circle are still present in the output expression.

c(kT) tracks the unit step perfectly after 3 sampling periods (first term has a non unity coefficient). The output response is shown in Figure 1.

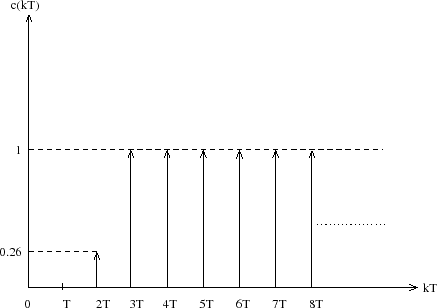$\begin{figure} \centering \input{deadbt.pstex_t} \end{figure}$

Figure 1: Deadbeat Response of The System in Example 1

If G_p(z) did not have any poles or zeros on or outside the unit circle it would take two sampling periods to track the step input when G_p(z) has two more poles than zeros.

Example 2:

Let us consider the plant transfer function as

For Unit Step Input:

G_p(z) has a zero at -2.8 and two poles at z = 1. The number of poles exceeds the number of zeros by one.

M(z) must contain the term 1 + 2.8 z ^-1 and 1- M(z) should contain (1- z ^-1 )² .

This implies

$\displaystyle M(z) = (1 + 2.8z^{ - 1} )(m_1z^{-1}+m_2 z^{ - 2})$

$\displaystyle 1 - M(z) = (1 - z^{ - 1} )^2(1 + a_1 z^{ - 1} )$

Combining the 2 equations and equating the like powers of z ^-1,

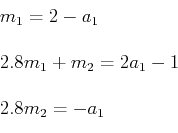
$\begin{displaymath} \begin{array}{l} m_1=2-a_1 \\ \\ 2.8 m_1 + m_2 = 2a_1 - 1 \\ \\ 2.8m_2 =-a_1 \\ \end{array} \end{displaymath}$

The solutions of the above equations are m₁ = 0.72 , m₂ = - 0.457 and a₁ = 1.28 . Thus

$\displaystyle M(z) = (0.72z^{-1}-0.457z^{ - 2}) (1 + 2.8z^{ - 1} )$

and

$\displaystyle 1 - M(z) = (1 - z^{ - 1} )^2(1 + 1.28z^{ - 1})$