Module 6 : Deadbeat Response Design

Lecture 2 : Deadbeat response design when some of the poles and zeros are on or outside the unit circle

 


P equals either the order of the poles of R(z) or the order of poles of Gp(z) at z = 1 which ever is greater. Truncation depends on the following.

1. The order of poles of M(z) and ( 1- M(z)) must be equal.

2. Total number of unknowns must be equal to the order of M(z) so that they can be solved independently.

Example 1:

Let us consider the plant transfer function as

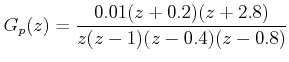
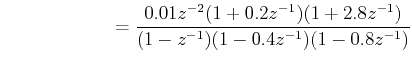
$\displaystyle G_p (z) = \frac{{0.01(z + 0.2)(z + 2.8)}}{{z(z - 1)(z - 0.4)(z - 0.8)}} $$\displaystyle \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = \frac{{0.01z^{ - 2} ... ... )(1 + 2.8z^{ - 1} )}}{{(1 - z^{ - 1} )(1 - 0.4z^{ - 1} )(1 - 0.8z^{ - 1} )}} $


For Unit Step Input:

Gp(z) has a zero at -2.8 and pole at z = 1. Therefore M(z) must contain the term 1 + 2.8 z -1 and ( 1- M(z)) should contain 1 - z -1 .

Gp(z) has two more poles than zeros. This implies

$\displaystyle M(z) = (1 + 2.8z^{ - 1} )m_2 z^{ - 2} $

$\displaystyle 1 - M(z) = (1 - z^{ - 1} )(1 + a_1 z^{ - 1} + a_2 z^{ - 2} ) $


Since minimum order of M(z) is 3, we have 3 unknowns in total. Combining the 2 equations


Thus

$\displaystyle M(z) = 0.26z^{ - 2} (1 + 2.8z^{ - 1} ) $


and

$\displaystyle 1 - M(z) = (1 - z^{ - 1} )(1 + z^{ - 1} + 0.73z^{ - 2} ) $


Putting the expressions of M(z) and ( 1- M(z)) in the controller equation




Thus