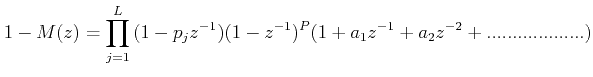There are some practical issues in deadbeat response design.

Dead beat response design depends on the cancellation of poles and zeros of the plant transfer function.

If the poles are on or outside the unit circle, imperfect cancellation may lead to instability.

Thus, for practical constraints, one should not attempt to cancel poles which are on or outside the unit circle.

1 Deadbeat response design when some of the poles and zeros are on or outside the unit circle

Let the plant transfer function be

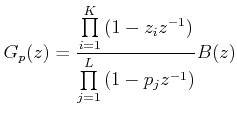
$\displaystyle G_p (z) = \frac{{\prod\limits_{i = 1}^K {(1 - z_i z^{ - 1} )} }}{{\prod\limits_{j = 1}^L {(1 - p_j z^{ - 1} )} }}A(z)$

where, K and L are the number of zeros and poles on or outside the unit circle and B(z) is a rational transfer function in z ^-1 with poles and zeros inside the unit circle. This implies

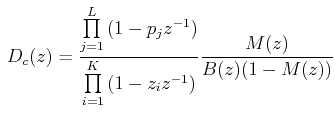
$\displaystyle \, D_c (z) = \frac{{\prod\limits_{j = 1}^L {(1 - p_j z^{ - 1} )} ... ...prod\limits_{i = 1}^K {(1 - z_i z^{ - 1} )} }}\frac{{M(z)}}{{A(z)(1 - M(z))}}$

Since we should not cancel poles or zeros which are on or outside unit circle by the controller D_c(z), we have to choose M(z) such that these get canceled out.

Thus M(z) must contain the factors

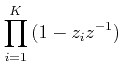
$\displaystyle {\prod\limits_{i = 1}^K {(1 - z_i z^{ - 1} )} }$

and ( 1- M(z)) must contain the factors

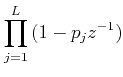
$\displaystyle {\prod\limits_{j = 1}^L {(1 - p_j z^{ - 1} )} }$

So,

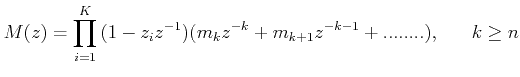
$\displaystyle M(z) = \prod\limits_{i = 1}^K {(1 - z_i z^{ - 1} )} (m_k z^{ - k} + m_{k + 1} z^{ - k - 1} + ........), \;\;\;\;\;\; k \ge n$

and

$\displaystyle 1 - M(z) = \prod\limits_{j = 1}^L {(1 - p_j z^{ - 1} )} (1 - z^{ - 1} )^P (1 + a_1 z^{ - 1} + a_2 z^{ - 2} + ...................)$