Module 4 : Time Response of discrete time systems

Lecture 1 : Time Response of discrete time systems

1 Time Response of discrete time systems

Absolute stability is a basic requirement of all control systems. Apart from that, good relative stability and steady state accuracy are also required in any control system, whether continuous time or discrete time. Transient response corresponds to the system close loop poles and steady state response corresponds to the excitation poles or poles of the input function.

1.1 Time response specifications

In many practical control systems, the desired performance characteristics are specified in terms of time domain quantities. Unit step input is the most commonly used in analysis purpose of a system since it is easy to generate and represents a sufficiently drastic change thus provides useful information on both transient and steady state response.

The transient response of a system depends on the initial conditions. It is a common practice to consider the system initially at rest.
Consider the digital control system shown in Figure 1

Figure 1: Block Diagram of a closed loop digital system

Similar to the continuous time case, transient response of a digital control system can also be characterized by the following.

  1. 1. Rise time (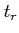$ t_r$): Time required for the unit step response to rise from 0% to 100% of its final value in case of underdamped system or 10% to 90% of its final value in case of overdamped system.


  2. 2. Delay time (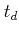$ t_d$): Time required for the the unit step response to reach 50\% of its final value.


  3. 3. Peak time (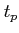$ t_p$): Time at which maximum peak occurs.


  4. 4. Peak overshoot (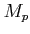$ M_p$): The difference between the maximum peak and the steady state value of the unit step response.


  5. 5. Settling time ($ t_s$): Time required for the unit step response to reach and stay within 2% or 5% of its steady state value.

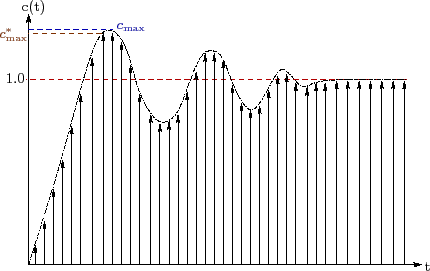
However since the output response is discrete the calculated performance measures may be slightly different from the actual values. Figure 2 illustrates this. The output has a maximum value $ c_{\max}$ whereas the maximum value of the discrete output is $ c^*_{\max}$ which is always less than or equal to $ c_{\max}$. If the sampling period is small enough compared to the oscillations of the response then this difference will be small otherwise $ c^*_{\max}$ may be completely erroneous.

Figure 2: Unit step response of a discrete time system
\begin{figure}\centering \input{m4l1f3.pstex_t}\end{figure}