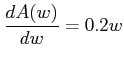Looking at the correspondence between w -plane and z -plane, when an all zero row occurs, we can conclude that following two scenarios are likely to happen.

. Pairs of real roots in the z -plane that are inverse of each other.

. Pairs of roots on the unit circle simultaneously.

Example 4:

Consider the characteristic equation

$\displaystyle P(z) = z^3 - 1.7 z^2-z+0.8=0$

Transforming P(z) into w -domain:

$\displaystyle Q(w) = \left [ \frac {w+1}{w-1} \right ]^{3}-1.7\left [ \frac {w+1}{w-1} \right ]^{2}-\left [ \frac {w+1}{w-1} \right ]+0.8=0$

or, $\displaystyle \;\; Q(w) = 0.9 w^3 + 0.1 w^2 -8.1 w -0.9 = 0$

The Routh array:

The tabulation ends here. The auxiliary equation is formed by using the coefficients of w² row, as:

$\displaystyle A(w) = 0.1 w^2 - 0.9=0$

Taking the derivative,

$\displaystyle \dfrac{dA(w)}{dw} = 0.2 w$