1 Stability Analysis using Bilinear Transformation and Routh Stability Criterion

Another frequently used method in stability analysis of discrete time system is the bilinear transformation coupled with Routh stability criterion. This requires transformation from z -plane to another plane called w -plane.

The bilinear transformation has the following form.

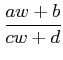
$\displaystyle z$ $\displaystyle =$ $\displaystyle \frac {aw+b}{cw+d}$

where a, b, c, d are real constants. If we consider a = b = c = 1 and d = - 1, then the transformation takes a form

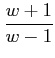
$\displaystyle z$ $\displaystyle =$ $\displaystyle \frac {w+1}{w-1}$

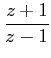
or, $\displaystyle \;\; w$ $\displaystyle =$ $\displaystyle \frac {z+1}{z-1}$

This transformation maps the inside of the unit circle in the z -plane into the left half of the w -plane.

Let the real part of w be α and imaginary part be &beta.

$\Rightarrow w=\alpha+j\beta$ . The inside of the unit circle in z -plane can be represented by:

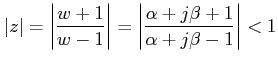
$\displaystyle \vert z\vert= \left \vert\frac{w+1}{w-1} \right \vert= \left \vert\frac {\alpha+j\beta+1}{\alpha+j\beta-1}\right \vert< 1$

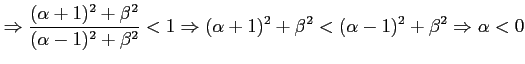
$\displaystyle \Rightarrow \frac{(\alpha+1)^2+\beta^{2}}{(\alpha-1)^{2}+\beta^{2... ...htarrow (\alpha+1)^{2}+\beta^{2}<(\alpha-1)^{2}+\beta^{2} \Rightarrow \alpha<0$

Thus inside of the unit circle in z -plane maps into the left half of w -plane and outside of the unit circle in z -plane maps into the right half of w -plane. Although w -plane seems to be similar to s -plane, quantitatively it is not same.

In the stability analysis using bilinear transformation, we first substitute 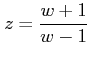$z=\dfrac{w+1}{w-1}$ in the characteristics equation P(z) = 0 and simplify it to get the characteristic equation in w -plane as Q(w) = 0. Once the characteristics equation is transformed as Q(w) = 0, Routh stability criterion is directly used in the same manner as in a continuous time system.