Example 3:
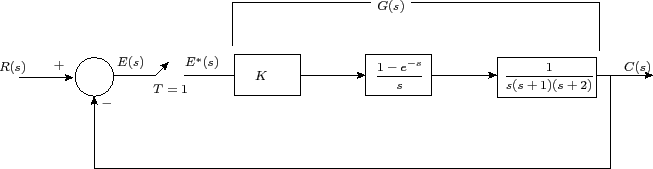
Consider the system shown in Figure 1. Find out the range of K for which the system is stable.
Solution:
 |
Characteristic equation:
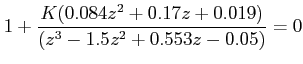
Transforming P(z) into w -domain:
![$\displaystyle Q(w) = \left [ \frac {w+1}{w-1} \right ]^{3}+(0.084K-1.5)\left [ ...
...1} \right ]^{2}+(0.17K+0.553)\left [ \frac {w+1}{w-1} \right ]+(0.019K-0.05)=0 $](images/img54.png)
or, ![]()
We can now construct the Routh array as
Module 3 : Stability Analysis of Discrete Time Systems
Lecture 2 : Stability Analysis using Bilinear Transformation and Routh Stability Criterion
Consider the system shown in Figure 1. Find out the range of K for which the system is stable.
Solution:
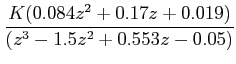
 |
Characteristic equation:
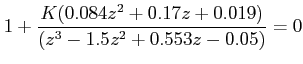
Transforming P(z) into w -domain:
![$\displaystyle Q(w) = \left [ \frac {w+1}{w-1} \right ]^{3}+(0.084K-1.5)\left [ ...
...1} \right ]^{2}+(0.17K+0.553)\left [ \frac {w+1}{w-1} \right ]+(0.019K-0.05)=0 $](images/img54.png)
or, ![]()
We can now construct the Routh array as