The system will be stable if all the elements in the first column have same sign. Thus the conditions for stability, in terms of K, are

$\displaystyle 0.003+0.27K > 0$	$\displaystyle \Rightarrow$	$\displaystyle K>-0.011$
$\displaystyle 1.1-0.11K >0$	$\displaystyle \Rightarrow$	$\displaystyle K <10$
$\displaystyle 0.01K^2-1.55K+4.17>0$	$\displaystyle \Rightarrow$	$\displaystyle K<2.74 \;\;\;$ or, $\displaystyle \;\;\; K>140.98$
$\displaystyle 3.1+0.07K > 0$	$\displaystyle \Rightarrow$	$\displaystyle K>-44.3$

Combining above four constraints, the stable range of K can be found as

$\displaystyle -0.011<K<2.74$

1.1 Singular Cases

In Routh array, tabulation may end in occurance with any of the following conditions.

. The first element in any row is zero

. All the elements in a single row are zero.

The remedy of the first case is replacing zero by a small number ε and then proceeding with the tabulation. Stability can be checked for the limiting case. Second singular case indicates one or more of the following cases.

. Pairs of real roots with opposite signs.

. Pairs of imaginary roots.

. Pairs of complex conjugate roots which are equidistant from the origin.

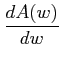When a row of all zeros occurs, an auxiliary equation A(w)= 0 is formed by using the coefficients of the row just above the row of all zeros. The roots of the auxiliary equation are also the roots of the characteristic equation. The tabulation is continued by replacing the row of zeros by the coefficients of $\dfrac{dA(w)}{dw}$ .