The present worth of the uniform gradient series will be located at the beginning i.e. in year ‘0’ i.e. 2 years before the commencement of the uniform gradient.
Now the equivalent present worth (in Rs.) of Option-1 is calculated as follows;
PW1 = - 25,00,000 - 45,000 (P/A, i, n) - 3000 (P/G, i, n) + 1,20,000 (P/A, i, n) + 5,50,000 (P/F, i, n)
PW1 = - 25,00,000 - 45,000 (P/A, 8%, 10) - 3000 (P/G, 8%, 10) + 1,20,000 (P/A, 8%, 10) + 550000 (P/F, 8%, 10)
PW1 = - 25,00,000 + (1,20,000 - 45,000) (P/A, 8%, 10) - 3000 (P/G, 8%, 10) + 5,50,000 (P/F, 8%, 10)
Now putting the values of different compound interest factors (the expressions in terms of ‘i’ and ‘n’ already stated in Module-1) in the above expression for PW1 results in the following;
PW1 = - 25,00,000 + 75,000 X 6.7101 - 3000 X 25.9768 + 5,50,000 X 0.4632
PW1 = - 25,00,000 + 50,3258 - 77,930 + 25,4760
PW1 = - Rs.18,19,912
The cash flow diagram of Option-2 is shown in Fig. 2.7.
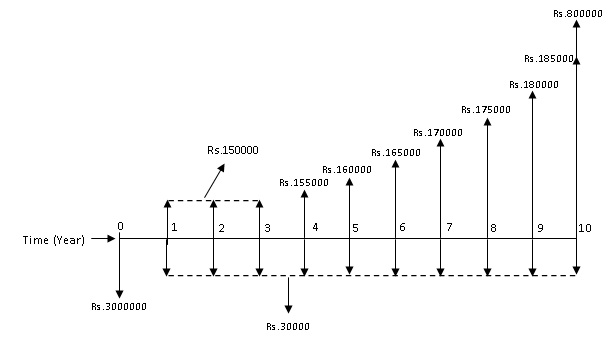
Fig. 2.7 Cash flow diagram of Option-2
For Option-2, the annual income is in the form of a positive uniform gradient series with gradient starting from end of year ‘4’. The annual income can be split into the uniform base amount of Rs.1,50,000 and the gradient amount in multiples of Rs.5000 starting from end of year ‘4’ and is shown in Fig. 2.8.
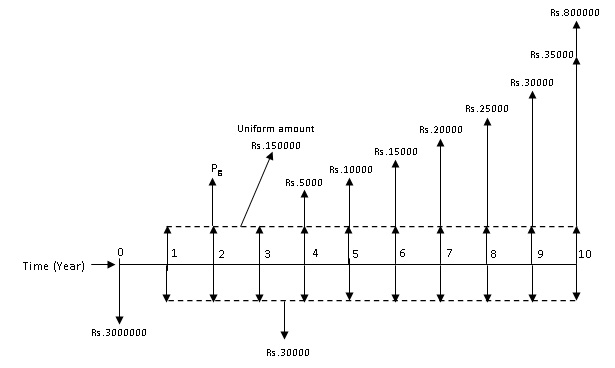
Fig. 2.8 Cash flow diagram of Option-2 with annual income split into uniform base amount and gradient amount
The equivalent present worth of the gradient series (of the annual income) starting from end of year ‘4’ will be located at the end of year ‘2’ i.e. 2 years before the start of the gradient. Further the present worth of this amount at beginning i.e. at time ‘0’ will be obtained by multiplying the equivalent present worth ‘Pg’ (shown in Fig. 2.8)at the end of year ‘2’ (which is a future amount) with the single payment present worth factor (P/F, i, n).
Now the equivalent present worth (in Rs.) of Option-2 is determined as follows;
PW2 = - 3000000 - 30000(P/A, 8%, 10) + 150000(P/A, 8%, 10) + Pg (P/F, 8%, 2) + 800000(P/F, 8%, 10)
Now in the above expression, Pg will be replaced by G (P/G, i, n) i.e. 5000(P/G, 8%, 8).
PW2 = - 3000000 - 30000(P/A, 8%, 10) + 150000(P/A, 8%, 10) + 5000(P/G, 8%, 8) (P/F, 8%, 2) + 800000(P/F, 8%, 10)
PW2 = - 3000000 + (150000 - 30000) (P/A, 8%, 10) + 5000(P/G, 8%, 8) (P/F, 8%, 2) + 800000 (P/F, 8%, 10)
Now putting the values of different compound interest factors in the above expression for PW2 results in the following;
PW2= - 3000000 + 120000 X 6.7101 + 5000 X 17.8061 X 0.8573 + 800000 X 0.4632
PW2= - 3000000 + 805212 + 76326 + 370560
PW2 = - Rs.1747902