Now the equivalent present worth of Alternative-2 i.e. PW2 (in Rs.) is calculated as follows;
The initial cost, P = Rs.2,00,000 (cash outflow),
Annual operating and maintenance cost, A = Rs.35,000 (cash outflow),
Salvage value, F = Rs.70,000 (cash inflow).
PW2 = - 2,00,000 - 35,000(P/A, i, n) + 70,000(P/F, i, n)
PW2 = - 2,00,000 - 35,000(P/A, 10%, 5) + 70,000(P/F, 10%, 5)
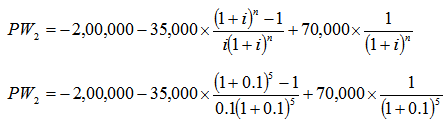
PW2 = - 2,00,000 - 35,000 X 3.7908 + 70,000 X 0.6209
PW2 = - 2,00,000 - 13,2678 + 43,463
PW2= - Rs.2,89,215
Comparing the equivalent present worth of both the alternatives, it is observed that Alternative-2 will be selected as it shows lower negative equivalent present worth compared to Alternative-1 at the interest rate of 10% per year.
The equivalent present worth of both the alternatives can also be calculated by using the values of compound interest factors from interest tables. The equivalent present worth of Alternative-1 i.e. PW1 is calculated as follows;
PW1 = - 3,00,000 – 20,000 (P/A, i, n ) + 1,25,000 (P/F, i, n )
PW1 = - 3,00,000 – 20,000 (P/A, 10%, 5 ) + 1,25,000 (P/F, 10%, 5 )
The values of compound interest factors i.e. (P/A, i, n) and (P/F, i, n) can be obntained from the interest tables (discrete compounding) available in texts cited in the list of references [1, 7, 14]. Now referring to the interest table for 10% interest rate, the values of compound interest factors i.e. (P/A, 10%, 5) and (P/F, 10%, 5) at interest rate (‘i' ) of 10% and for interest period (‘n' ) of 5 years are obtained at the intersection of these factors and interest period ‘n' equal to 5 i.e. the values are obtained from P/A column and P/F column at ‘n' equal to 5 from the interest table (discrete compounding) corresponding to 10% interest rate. The obtained values of (P/A, 10%, 5) and (P/F, 10%, 5) are 3.7908 and 0.6209 respectively (same as those obtained using mathematical expressions of these factors).
Now putting the values of compound interest factors in the above expression, the equivalent present worth of Alternative-1 i.e. PW1 is calculated as follows;
![]()
PW1 = - 3,00,000 -75,816 + 77,613
PW1 = - Rs.2,98,203
Now the calculation of equivalent present worth of Alternative-2 i.e. PW2 (in Rs.) is presented below.
PW2 = - 2,00,000 – 35,000 (P/A, i, n ) + 70,000 (P/F, i, n )
PW2 = - 2,00,000 – 35,000 (P/A, 10%, 5 ) + 70,000 (P/F, 10%, 5 )
Now putting the values of compound interest factors in the above expression (same as above) the equivalent present worth of Alternative-2 i.e. PW2 is calculated as follows;
![]()
PW2 = - 2,00,000 – 1,32,678 + 43,463
PW2 = - Rs.2,89,215
It may be noted that in the above example only cost components and the salvage value of the alternatives were considered for comparison. In the next example, same problem as mentioned in Example-1 will be discussed by taking into account the annual revenues of the alternatives.
Example -2
Alternative-1: Initial purchase cost = Rs.3,00,000, Annual operating and maintenance cost = Rs.20000, Expected salvage value = Rs.1,25,000, Useful life = 5 years.
Alternative-2: Initial purchase cost = Rs.2,00,000, Annual operating and maintenance cost = Rs.35000, Expected salvage value = Rs.70,000, Useful life = 5 years.
The annual revenue to be generated from production of concrete (by concrete mixer) from Alternative-1 and Alternative-2 are Rs.50,000 and Rs.45,000 respectively. Compute the equivalent present worth of the alternatives at the same rate of interest as in Example-1 i.e. 10% per year and find out the economical alternative.
Solution:
The cash flow diagram of Alternative-1 is shown in Fig. 2.3.
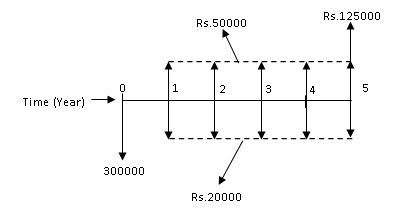
Fig. 2.3 Cash flow diagram of Alternative-1
The equivalent present worth of Alternative-1 is calculated as follows;
PW1 = - 3,00,000 - 20,000 (P/A, i, n) + 50,000 (P/A, i, n) + 1,25,000 (P/F, i, n)
PW1 = - 3,00,000 - 20,000 (P/A, 10%, 5) + 50,000 (P/A, 10%, 5) + 1,25,000 (P/F, 10%, 5)
PW1 = - 3,00,000 + (50,000 – 20,000) (P/A, 10%, 5) + 1,25,000 (P/F, 10%, 5)
PW1= - 3,00,000 + 30,000 (P/A, 10%, 5) + 1,25,000 (P/F, 10%, 5)
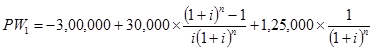
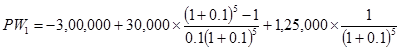
PW1 = - 2,00,000 - 35,000 X 3.7908 + 70,000 X 0.6209
PW1 = - 3,00,000 + 1,13,724 + 77,613
PW1 = - Rs.1,08,663