Fuel consumption models are mathematical functions relating the various factors
contributing to the fuel consumption.
The influencing factors may be no. of vehicle trips, distance travelled by the
vehicle, no. of stops, vehicle’s average speed, etc.
The major fuel consumption models are discussed in the following sections.
Average speed models are macroscopic in nature.
They are concerned with the traffic network as a whole, on a large scale.
Individual vehicles are not considered.
This model relates the fuel consumption directly with the travel time (or
indirectly with vehicle speeds).
This model is not valid for speeds higher than 56 km/hr. as the effects of air
resistance become increasingly stronger.
The fuel consumed is related to the average speed (or travel time) using the
relation below:
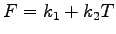 |
|
|
(1) |
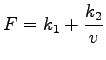 |
|
|
(2) |
where, 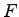 = Fuel consumed per vehicle per unit distance (liters/km), = Fuel consumed per vehicle per unit distance (liters/km), 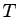 =
Travel time per unit distance, including stops and speed changes (minutes/km), =
Travel time per unit distance, including stops and speed changes (minutes/km),
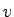 = Avg. speed measured over a distance including stops and speed changes = Avg. speed measured over a distance including stops and speed changes
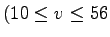 kmph), kmph), 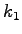 = parameter associated with fuel consumed to
overcome rolling resistance, approximately proportional to vehicle weight
(liters/veh- km), = parameter associated with fuel consumed to
overcome rolling resistance, approximately proportional to vehicle weight
(liters/veh- km), 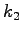 = Parameter approximately proportional to fuel
consumption while idling (liters/hr).Fig. 1 gives the relation between fuel and
consumption and speed of the vehicle.
It can be inferred from the figure that fuel consumption is high for lower
speeds and is the minimum for intermediate speeds. = Parameter approximately proportional to fuel
consumption while idling (liters/hr).Fig. 1 gives the relation between fuel and
consumption and speed of the vehicle.
It can be inferred from the figure that fuel consumption is high for lower
speeds and is the minimum for intermediate speeds.
Figure 1:
Fuel consumption as a function of speed
![\begin{figure}
\centerline{\epsfig{file=qfFuelConsumptionVsSpeed.eps,width=8cm}}
%, Source: [4]}
\end{figure}](img9.png) |
Fig. 2 shows the relation between bus fuel
consumption and number of stops.
It is clear from the graph that fuel consumption increases as the number of
stops of the vehicle increases.
Figure 2:
Bus fuel consumption as a function of stops
![\begin{figure}
\centerline{\epsfig{file=qfFuelConsumptionVsStops.eps,width=8cm}}
%, Source: [1]}
\end{figure}](img10.png) |
A city has a total of 20000 commuters travelling at an average speed of 25kmph,
and using an arterial road of length 15 km.
Due to the congestion and parking problems, 35% commuters form car pools with
a car occupancy of 3.0 and 20% arrange for subscription bus service (50
seater).
Rest of the commuters choose to travel by private cars.
The peak period congestion was found to be reduced and the speed was increased
to 35kmph.
Assuming the no. of stops to be 7, calculate the amount of fuel saved.
Take 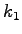 = 0.085liters/km, = 0.085liters/km, 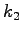 = 1.5 liters/hr.
It is required to find the difference in fuel consumption between the two
cases.
In the first case, all commuters use private cars (i.e. car occupancy 1) and in
the second case, some of them use public transport services, while others still
use private cars. = 1.5 liters/hr.
It is required to find the difference in fuel consumption between the two
cases.
In the first case, all commuters use private cars (i.e. car occupancy 1) and in
the second case, some of them use public transport services, while others still
use private cars.
In the first case, there were a total of 20000 commuters with car occupancy =
1, speed 25kmph and the distance to be travelled is 15 km. from the
equation 1, we have:
Total fuel consumption,
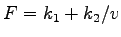 .
Thus for the distance of 15km travelled, the total fuel consumption is equal to
[0.085 * 15] + [(1.5/25) * 15], which is 2.175 liters/vehicle.
Thus for a total of 20000 commuters, the fuel consumption will be 2.175 * 20000
which is equal to 43500 liters. .
Thus for the distance of 15km travelled, the total fuel consumption is equal to
[0.085 * 15] + [(1.5/25) * 15], which is 2.175 liters/vehicle.
Thus for a total of 20000 commuters, the fuel consumption will be 2.175 * 20000
which is equal to 43500 liters.
In the second case, the vehicles move with a new speed of 35kmph, and out of
the total 20000 commuters, 35% (0.35 * 20000 = 7000) form car pools with
occupancy 3.0.
Hence, the number of car pool vehicles is 7000/3, that is 2333 vehicles. 20%
(0.20 * 20000 = 4000) of the commuters use a 50 seater bus service.
Hence the number of buses will be 4000/50, which is equal to 80 buses.
Remaining (20000 - 7000 - 4000 = 9000) are single car drivers.
The total consumption by car will include the consumption of cars of single
occupancy and the cars in the car pool.
Hence, the fuel consumption by cars is [0.085 * 15] + [(1.5/35) * 15], that is
1.917 liters/vehicles.
So, for all the cars, the total fuel consumption will be 1.917* (9000 + 2333),
which is 21725.36 liters.
Similarly, the bus fuel consumption for a bus with 7 stops will be 0.3 *2.35 *
80 * 15 which is 846 liters.
Fuel consumption corresponding to 7 stops is obtained from
Fig. 2.
2.35 is a conversion factor to bring the fuel consumption in terms of liters/km
instead of gallons/mile.
Total fuel consumption will be the sum of fuel consumptions of bus and car.
That is 21725+846 = 22571 liters.
The total amount of fuel saved will be the difference of fuel consumptions in
both the cases.
Hence the amount of fuel saved is 43500 - 2257, which is equal to 20929 liters.
|