| |
| | |
|
Cycle time is the time taken by a signal to complete one full cycle of
iterations. i.e. one complete rotation through all signal indications.
It is denoted by 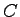 .
The way in which the vehicles depart from an intersection when the green signal
is initiated will be discussed now.
Figure 1 illustrates a group of N vehicles at a signalized
intersection, waiting for the green signal. .
The way in which the vehicles depart from an intersection when the green signal
is initiated will be discussed now.
Figure 1 illustrates a group of N vehicles at a signalized
intersection, waiting for the green signal.
Figure 1:
Group of vehicles at a signalized intersection waiting for green
signal
 |
As the signal is initiated, the time interval between two vehicles, referred as
headway, crossing the curb line is noted.
The first headway is the time interval between the initiation of the green
signal and the instant vehicle crossing the curb line.
The second headway is the time interval between the first and the second
vehicle crossing the curb line.
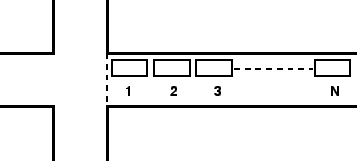
Successive headways are then plotted as in figure 2.
Figure 2:
Headways departing signal
 |
The first headway will be relatively longer since it includes the reaction time
of the driver and the time necessary to accelerate.
The second headway will be comparatively lower because the second driver can
overlap his/her reaction time with that of the first driver's.
After few vehicles, the headway will become constant.
This constant headway which characterizes all headways beginning with the
fourth or fifth vehicle, is defined as the saturation headway, and is denoted
as 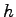 .
This is the headway that can be achieved by a stable moving platoon of vehicles
passing through a green indication.
If every vehicles require .
This is the headway that can be achieved by a stable moving platoon of vehicles
passing through a green indication.
If every vehicles require 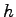 seconds of green time, and if the signal were
always green, then seconds of green time, and if the signal were
always green, then 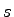 vehicles per hour would pass the intersection.
Therefore, vehicles per hour would pass the intersection.
Therefore,
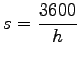 |
(1) |
where 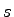 is the saturation flow rate in vehicles per hour of green time per
lane, is the saturation flow rate in vehicles per hour of green time per
lane, 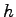 is the saturation headway in seconds.
As noted earlier, the headway will be more than h particularly for the first
few vehicles.
The difference between the actual headway and h for the is the saturation headway in seconds.
As noted earlier, the headway will be more than h particularly for the first
few vehicles.
The difference between the actual headway and h for the 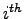 vehicle and is
denoted as vehicle and is
denoted as 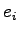 shown in figure 2.
These differences for the first few vehicles can be added to get start up lost
time, shown in figure 2.
These differences for the first few vehicles can be added to get start up lost
time, 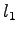 which is given by, which is given by,
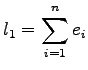 |
(2) |
The green time required to clear N vehicles can be found out as,
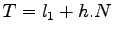 |
(3) |
where 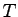 is the time required to clear N vehicles through signal, is the time required to clear N vehicles through signal, 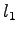 is the
start-up lost time, and is the
start-up lost time, and 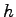 is the saturation headway in seconds.
Effective green time is the actual time available for the vehicles to cross the
intersection.
It is the sum of actual green time ( is the saturation headway in seconds.
Effective green time is the actual time available for the vehicles to cross the
intersection.
It is the sum of actual green time (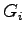 ) plus the yellow minus the applicable
lost times.
This lost time is the sum of start-up lost time ( ) plus the yellow minus the applicable
lost times.
This lost time is the sum of start-up lost time (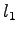 ) and clearance lost time
( ) and clearance lost time
(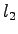 ) denoted as ) denoted as 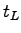 .
Thus effective green time can be written as, .
Thus effective green time can be written as,
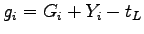 |
(4) |
The ratio of effective green time to the cycle length (
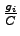 )is
defined as green ratio.
We know that saturation flow rate is the number of vehicles that can be moved
in one lane in one hour assuming the signal to be green always.
Then the capacity of a lane can be computed as, )is
defined as green ratio.
We know that saturation flow rate is the number of vehicles that can be moved
in one lane in one hour assuming the signal to be green always.
Then the capacity of a lane can be computed as,
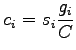 |
(5) |
where 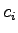 is the capacity of lane in vehicle per hour, is the capacity of lane in vehicle per hour, 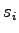 is the
saturation flow rate in vehicle per hour per lane, is the
saturation flow rate in vehicle per hour per lane, 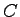 is the cycle time in
seconds.
Let the cycle time of an intersection is 60 seconds, the green time for a phase
is 27 seconds, and the corresponding yellow time is 4 seconds.
If the saturation headway is 2.4 seconds per vehicle, the start-up lost time is 2
seconds per phase, and the clearance lost time is 1 second per phase, find the capacity
of the movement per lane?
Total lost time, is the cycle time in
seconds.
Let the cycle time of an intersection is 60 seconds, the green time for a phase
is 27 seconds, and the corresponding yellow time is 4 seconds.
If the saturation headway is 2.4 seconds per vehicle, the start-up lost time is 2
seconds per phase, and the clearance lost time is 1 second per phase, find the capacity
of the movement per lane?
Total lost time, 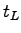 = 2+1 = 3 seconds.
From equation 4
effective green time, = 2+1 = 3 seconds.
From equation 4
effective green time, 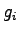 = 27+4-3 = 28 seconds.
From equation 1
saturation flow rate, = 27+4-3 = 28 seconds.
From equation 1
saturation flow rate,
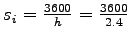 = 1500 veh per hr.
Capacity of the given phase can be found out from equation 5 as = 1500 veh per hr.
Capacity of the given phase can be found out from equation 5 as
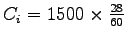 = 700 veh per hr per lane.
During any green signal phase, several lanes on one or more approaches are
permitted to move.
One of these will have the most intense traffic.
Thus it requires more time than any other lane moving at the same time.
If sufficient time is allocated for this lane, then all other lanes will also
be well accommodated.
There will be one and only one critical lane in each signal phase.
The volume of this critical lane is called critical lane volume. = 700 veh per hr per lane.
During any green signal phase, several lanes on one or more approaches are
permitted to move.
One of these will have the most intense traffic.
Thus it requires more time than any other lane moving at the same time.
If sufficient time is allocated for this lane, then all other lanes will also
be well accommodated.
There will be one and only one critical lane in each signal phase.
The volume of this critical lane is called critical lane volume.
|
|
| | |
|
|
|