| |
| | |
|
A new suburban freeway is designed in the level terrain.
Peak hour volume is 4,000 veh/h and the flow consists of 15% trucks and 3%
recreational vehicles (RV's).
The traffic is commuter type with peak hour factor 0.85 and interchange density
as 0.9 interchanges per kilometer.
Lane width is proposed to be 3.6 m with lateral clearance of 1.8 m.
How many lanes are needed to provide LOS C during the peak hour?
Assumptions: Assume 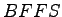 of 120 km/h. Since the freeway is being designed in a
suburban area assume that the number of lanes affects free-flow speed.
For commuter traffic we can take of 120 km/h. Since the freeway is being designed in a
suburban area assume that the number of lanes affects free-flow speed.
For commuter traffic we can take 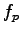 = 1.00.
We can get the corresponding values of adjustment factors from the tables as - = 1.00.
We can get the corresponding values of adjustment factors from the tables as -
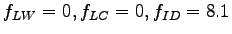 and and 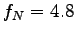 .
Find .
Find 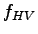 using equation using equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) as given below: as given below:
Convert volume (veh/h) to flow rate (pc/h/ln) using equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) .
Consider a four lane option, for four lane .
Consider a four lane option, for four lane 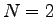 , keeping value of , keeping value of 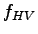 and and
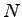 in equation in equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) we get we get 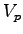 as: as:
Four lane option is not acceptable as 2544 pc/h/ln exceeds capacity of 2400 pc/h/ln.
Here 2400 pc/h/ln is the capacity of a single lane under standard conditions.
Consider a six lane option
Compute FFS for a six-lane freeway from equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) and
putting the respective values of adjustment factors we get and
putting the respective values of adjustment factors we get 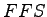 as: as:
Determine density from equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png)
Since,
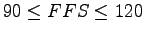 and and
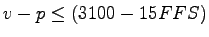 we can take we can take 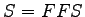 (from equation
(from equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ) Putting values of ) Putting values of 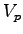 and and 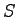 we get
density as we get
density as
Check the LOS, for the calculated value of density we can get the level of
service from the LOS table;
i.e for 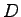 = 15.8 pc/km/ln we get LOS = C.
Hence number of lanes to be provided to satisfy LOS C during peak hour = 6. = 15.8 pc/km/ln we get LOS = C.
Hence number of lanes to be provided to satisfy LOS C during peak hour = 6.
|
|
| | |
|
|
|