| |
| | |
|
Consider an existing four lane freeway in rural area, having very restricted
geometry with rolling terrain.
Peak hour volume is 2000 veh/h with 5% trucks.
The traffic is commuter type with peak hour factor 0.92 and interchange density
as 0.6 interchanges per kilometer.
Freeway consists of two lanes in each direction of 3.3 m width with lateral
clearance of 0.6 m.
Find the LOS of freeway during peak hour.
Assumptions: Assume 0 percent buses and RVs since none are indicated.
Assume BFFS of 120 km/h for rural areas.
Since the freeway is in a rural area assume that the number of lanes does not
affect free-flow speed.
Assume 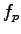 = 1.00 for commuter traffic.
We can get the corresponding values of adjustment factors from the tables as - = 1.00 for commuter traffic.
We can get the corresponding values of adjustment factors from the tables as -
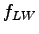 =3.1, =3.1, 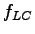 =3.9, =3.9, 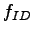 =3.9 and =3.9 and 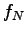 =0.
Find =0.
Find 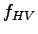 using equation using equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) as given below - as given below -
Convert volume (veh/h) to flow rate (pc/h/ln) using equation as given below
Compute free-flow speed from equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) as given below and
putting the respective values of adjustment factors we get as given below and
putting the respective values of adjustment factors we get 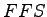 as as
Determine the density using the equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) as - as -
Since,
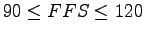 and and
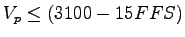 we can take we can take 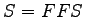 (from equation
(from equation ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ).
Keeping values of ).
Keeping values of 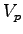 and and 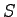 we can get the value of density as - we can get the value of density as -
Find Level of service, for the calculated value of density we can get the level
of service from the LOS table.
i.e for 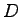 = 10.7 pc/km/ln we get LOS = B = 10.7 pc/km/ln we get LOS = B
|
|
| | |
|
|
|