From the law of sine,

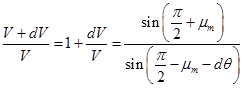(4.5.12)

Use trigonometric identities and Taylor series expansion, Eq. (4.5.12) can be simplified as below;

(4.5.13)

Since, , so the Eq. (4.5.13) can be simplified and integrated further from region ‘1' to ‘2',

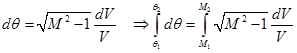(4.5.14)

From the definition of Mach number,

(4.5.15)

For a calorically perfect gas, the energy equation can be written as,

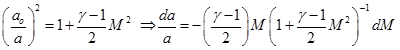(4.5.16)

Use Eqs (4.5.15 & 4.5.16) in Eq. (4.5.14) and integrate from ,

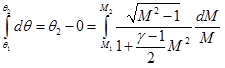(4.5.17)

The integral in the Eq. (4.5.18) is known as Prandtl-Meyer function , .

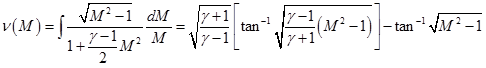(4.5.18)

Finally, Eq. (4.5.17) reduces to,

(4.5.19)

Thus, for a given upstream Mach number , one can obtain , subsequently calculate using given . Since, the expansion process is isentropic, the flow properties can be calculated from isentropic relations.