The continuity equation for oblique shock is,
 |
(4.5.1) |
Considering steady flow with no body forces, the momentum equation can be resolved in tangential and normal directions.
 |
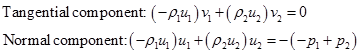(4.5.2) |
Substitute Eq. (4.5.1) in Eq. (4.5.2),
 |
(4.5.3) |
Thus, it is seen that the tangential component of flow velocity does not change across an oblique shock.
Finally, the energy equation gives,
 |
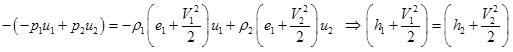(4.5.4) |
From the geometry of the Fig. 4.5.2, 
, hence
 |
(4.5.5) |
So, the energy equation becomes,
 |
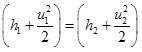(4.5.6) |
Examining the Eqs (4.5.1, 4.5.3 and 4.5.6), it is noted that they are identical to governing equations for a normal shock. So, the flow properties changes in the oblique shock are governed by the normal component of the upstream Mach number. So, the similar expressions can be written across an oblique shock in terms of normal component of free stream velocity i.e.
 |
|
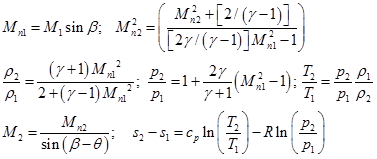Thus, the changes across an oblique shock are function of upstream Mach number 
and oblique shock angle 
while the normal shock is a special case when 
.
Referring to geometry of the oblique shock (Fig. 4.5.2-b),
 |
(4.5.8) |
Since, 
, Eq. (4.5.8) reduces to,
 |
(4.5.9) |
Use the relations given in Eq. (4.5.7) and substituting them in Eq. (4.5.9), the trigonometric equation becomes,
 |
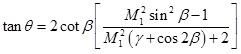(4.5.10) |