Oblique Shock Wave

The normal shock waves are straight in which the flow before and after the wave is normal to the shock. It is considered as a special case in the general family of oblique shock waves that occur in supersonic flow. In general, oblique shock waves are straight but inclined at an angle to the upstream flow and produce a change in flow direction as shown in Fig. 4.5.1(a). An infinitely weak oblique shock may be defined as a Mach wave (Fig. 4.5.1-b). By definition, an oblique shock generally occurs, when a supersonic flow is ‘turned into itself” as shown in Fig. 4.5.1(c). Here, a supersonic flow is allowed to pass over a surface, which is inclined at an angle to the horizontal. The flow streamlines are deflected upwards and aligned along the surface. Since, the upstream flow is supersonic; the streamlines are adjusted in the downstream an oblique shock wave angle with the horizontal such that they are parallel to the surface in the downstream. All the streamlines experience same deflection angle across the oblique shock.

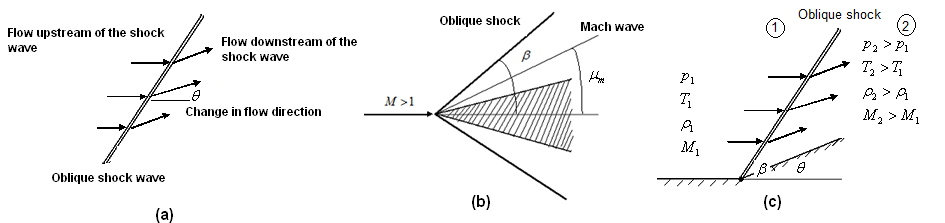
Fig. 4.5.1: Schematic representation of an oblique shock.

 

Oblique Shock Relations

Unlike the normal shocks, the analysis of oblique shocks is prevalent mainly in the two-dimensional supersonic flows. The flow field properties are the functions of as shown in Fig. 4.5.2. In the upstream of the shock, the streamlines are horizontal where, the Mach number and velocity of the flow are , respectively. The flow is deflected towards the shock in the downstream by angle θ such that the Mach number and velocity becomes , respectively. The components of , parallel and perpendicular to the shock are , respectively. Similarly, the analogous components for are, respectively. The normal and tangential Mach numbers ahead of the shock are while the corresponding Mach numbers behind the shock are, respectively.

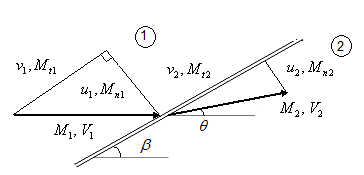
Fig. 4.5.2: Geometrical representation of oblique shock wave.