This equation is satisfied by for all values of θ. Since R is a constant, Eq. (3.7.3) may be interpreted as the equation of a circle with radius R with center at the origin. It is satisfied by for all values of R. Different values of R may be obtained by varying the uniform velocity and/or doublet strength. Hence, entire horizontal axis through the points A and B, extending infinitely far upstream and downstream, is a part of stagnation streamline. The above discussions can be summarized as follows;

• The dividing streamline 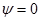that passes through the stagnation points A and B as shown in Fig. 3.7.1.

• The dividing streamline is a circle of radius R. The family of circles can be obtained by assigning different values of R with various doublet strength and free stream velocity.

• The flow inside the circle is generated from the doublet whereas flow outside the circle comes from the uniform flow. So, the flow inside the circle may be replaced by solid body and the external flow will not feel the difference.

• Thus, the inviscid, irrotational, incompressible flow over a circular cylinder of radius R can be simulated by adding a uniform flow of velocity and a doublet of strength and R is related to AND .

(3.7.4)

Referring to the Fig. 3.7.1, it is seen that the entire flow field is symmetrical about both horizontal and vertical axes through the center of the cylinder. It means the pressure distribution is also symmetrical about both the axes. When the pressure distribution over the top part of the cylinder is exactly balanced by the bottom part, there is no lift . Similarly, when the pressure distribution on the front part of the cylinder is exactly balanced by rear portion, then there is no drag. This is in contrast to the realistic situation i.e. a generic body placed in a flow field will experience finite drag and zero lift may be possible. This paradox between the theoretical result of zero drag in an inviscid flow and the knowledge of finite drag in real flow situation is known as d' Alembert's paradox .